
如图所示,公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E、M、F,M恰好为BC的中点,且E、F、M在同一直线上,在BE道路上停放着一排小汽车,从而无法直接测量B、E之间的距离,你能想出解决的方法吗?请说明其中的道理.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
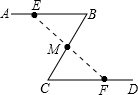 如图所示,公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E、M、F,M恰好为BC的中点,且E、F、M在同一直线上,在BE道路上停放着一排小汽车,从而无法直接测量B、E之间的距离,你能想出解决的方法吗?请说明其中的道理.
如图所示,公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E、M、F,M恰好为BC的中点,且E、F、M在同一直线上,在BE道路上停放着一排小汽车,从而无法直接测量B、E之间的距离,你能想出解决的方法吗?请说明其中的道理.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
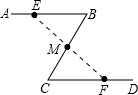
 如图所示,公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E、M、F,M恰好为BC的中点,且E、F、M在同一直线上,在BE道路上停放着一排小汽车,从而无法直接测量B、E之间的距离,你能想出解决的方法吗?请说明其中的道理.
如图所示,公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E、M、F,M恰好为BC的中点,且E、F、M在同一直线上,在BE道路上停放着一排小汽车,从而无法直接测量B、E之间的距离,你能想出解决的方法吗?请说明其中的道理.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:陕西省期末题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com