
 为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.分析 (1)根据三角形面积公式可得y2的解析式,再用长方形面积减去四个三角形面积,即可得y1的函数解析式;
(2)根据题意知y1=440,即即可得关于x的方程,解方程即可得;
(3)列出总费用的函数解析式,将其配方成顶点式,根据花的面积不大于440平方米可得x的范围,结合此范围根据二次函数性质即可得函数的最小值,从而得解.
解答 解:(1)根据题意,y2=2×$\frac{1}{2}$•x•x+2×$\frac{1}{2}$(40-x)(24-x)=2x2-64x+960,
y1=40×24-y2=-2x2+64x;
(2)根据题意,知y1=440,即-2x2+64x=440,
解得:x1=10,x2=22,
故当AN的长为10米或22米时种花的面积为440平方米;
(3)设总费用为W元,
则W=200(-2x2+64x)+100(2x2-64x+960)=-200(x-16)2+147200,
由(2)知当0<x≤10或22≤x≤24时,y1≤440,
在W=-200(x-16)2+147200中,当x<16时,W随x的增大而增大,当x>16时,W随x的增大而减小,
∴当x=0时,W取得最小值,最小值W=96000,
当x=24时,W取得最小值,最小值W=134400,
由于x=0无实际意义,
∴学校至少要准备134400元.
点评 本题主要考查二次函数的应用,理解题意列出相关的函数解析式是解题的根本,熟练掌握二次函数的性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 内错角相等 | |
| B. | 同位角互补,两直线平行 | |
| C. | 一个角的余角不等于其自身 | |
| D. | 在同一平面内,过一点能作且只能作一条直线与已知直线垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
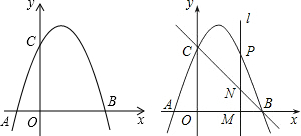
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
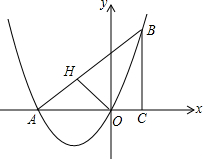 如图,在△ABC中,∠ACB=90°,BC=3,AC=3,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系,抛物线经过A、B、O三点.
如图,在△ABC中,∠ACB=90°,BC=3,AC=3,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系,抛物线经过A、B、O三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
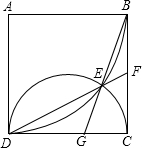 如图,在边长为1的正方形ABCD中,以A为圆心,AB为半径的弧与以DC为直径的半圆交于点E,连接DE并延长交BC于F,连接BE并延长交DC于G.
如图,在边长为1的正方形ABCD中,以A为圆心,AB为半径的弧与以DC为直径的半圆交于点E,连接DE并延长交BC于F,连接BE并延长交DC于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 9 | a | b | c | -5 | 1 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com