
【题目】如图,在平面直角坐标系中,已知A(﹣2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.
(1)求点O′的坐标;
(2)已知抛物线y=ax2+bx+c过A,B,C三点,且与⊙O′交于另一点E,求抛物线的解析式,并直接写出点E 坐标;
(3)设点P(t,0)是线段OB上一个动点,过点P作直线l⊥x轴,交线段BC于F,交抛物线y=ax2+bx+c于点G,请用t表示四边形BPCG的面积S;
(4)在(3)的条件下,四边形BPCG能否为平行四边形?若能,请求出t的值;若不能,请说明理由.
【答案】
(1)解:如图1中,连接CO′,设⊙O′的半径为R.

在Rt△OCO′中,∵OC2+OO2=CO′2,
∴42+(R﹣2)2=R2,
∴R=5,
∴OO′=5﹣2=3,
∴O′(3,0).
(2)解:∵A(﹣2,0),C(0,4),B(8,0),
∴  ,解得
,解得 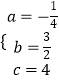 ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+4.
x+4.
易知E、C关于对称轴对称,
∴点E的纵坐标为4,
∴E(6,4)
(3)解:由题意G(t,﹣ ![]() t2+
t2+ ![]() t+4),
t+4),
∴S四边形BPCG= ![]() PG(Bx﹣Cx)=
PG(Bx﹣Cx)= ![]() (﹣
(﹣ ![]() t2+
t2+ ![]() t+4)8=﹣t2+6t+16(0<t<8)
t+4)8=﹣t2+6t+16(0<t<8)
(4)解:不可能是平行四边形.
理由:假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB﹣OP=2,
∴CE≠BP,
∴四边形BPCG不可能是平行四边形.
【解析】(1)如图1中,连接CO′,设⊙O′的半径为R.在Rt△OCO′中,根据OC2+OO2=CO′2,可得42+(R-2)2=R2,解方程求出求点O′的坐标;
(2)把A(-2,0),C(0,4),B(8,0)代入抛物线抛物线y=ax2+bx+c,求抛物线的解析式即点E 坐标;
(3)根据S四边形BPCG=![]() PG(Bx-Cx),即可用t表示四边形BPCG的面积S
PG(Bx-Cx),即可用t表示四边形BPCG的面积S
(4)不可能是平行四边形.假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB-OP=2,推出CE≠BP,即可得到所求结论..
【考点精析】本题主要考查了勾股定理的概念和平行四边形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.

(2)两条相交的直线OX、OY,使∠XOY=n,在射线OX、OY上分别再任意取A、B两点,作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,随着点A、B位置的变化,∠C的大小是否会变化?若保持不变,请求出∠C的度数;若发生变化,求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称____ ___,___ ;(2分)
(2)如图,已知格点(小正方形的顶点)![]() ,
,![]() ,
,![]() ,请你直接写出所有以格点为顶点,
,请你直接写出所有以格点为顶点,![]() 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形![]() 的顶点M的坐标。(3分)
的顶点M的坐标。(3分)

(3)如图,将![]() 绕顶点
绕顶点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,得到
,得到![]() ,连结
,连结![]() ,
,![]() .求证:
.求证:![]() ,即四边形
,即四边形![]() 是勾股四边形.(4分)
是勾股四边形.(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极支持鄂州市创建国家卫生城市工作,某商家计划从厂家采购A,B两种清洁产品共20件,产品的采购单价(元/件)是采购数量(件)的相关信息如下表所示.
采购数量(件) | 2 | 4 | 6 | … |
A产品单价(元) | 1460 | 1420 | 1380 | … |
B产品单价(元) | 1280 | 1260 | 1240 | … |
(1)设B产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ![]() ,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)该校打算通过“京东商城”网购20个A品牌的足球和3个B品牌的足球,“五一”期间商城打折促销,其中A品牌打八折,B品牌打九折,问:学校购买打折后的足球所花的费用比打折前节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
![]() 有一个角为
有一个角为![]() 的等腰三角形是等边三角形;
的等腰三角形是等边三角形;
![]() 等腰直角三角形一定是轴对称图形;
等腰直角三角形一定是轴对称图形;
![]() 有一条直角边对应相等的两个直角三角形全等;
有一条直角边对应相等的两个直角三角形全等;
![]() 到线段两端距离相等的点在这条线段的垂直平分线上.
到线段两端距离相等的点在这条线段的垂直平分线上.
正确的个数有![]()
![]()
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com