

 ,
,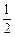 )或(
)或( ,
, )
) ="2," ∴OA=1,即A(1,0).
="2," ∴OA=1,即A(1,0).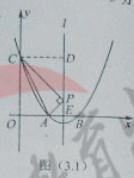
 .∴AE=OE-OA=
.∴AE=OE-OA= -1=
-1=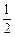 ,∵∠APC=90°,
,∵∠APC=90°, ,即
,即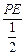
 ,解得PE=
,解得PE=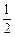 或PE=
或PE= ,
, ,
,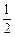 )或(
)或( ,
, )。(备注:可以用勾股定理或相似解答)
)。(备注:可以用勾股定理或相似解答)
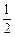 MN?t+
MN?t+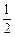 MN?(2-t)
MN?(2-t)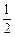 MN?(t+2-t)="MN=-" t2+2t(0<t<2),
MN?(t+2-t)="MN=-" t2+2t(0<t<2),

科目:初中数学 来源: 题型:
 男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).
男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).| 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).
男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5). ≈3.873)
≈3.873)查看答案和解析>>
科目:初中数学 来源:2009-2010学年浙江省衢州市开化二中九年级(下)第一次月考数学试卷(解析版) 题型:解答题
 ≈3.873)
≈3.873)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com