
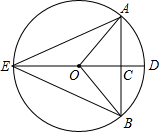
 如图,DE是⊙O的直径,弦AB⊥ED于C,连接AE、BE、AO、BO.则图中全等三角形的对数有
如图,DE是⊙O的直径,弦AB⊥ED于C,连接AE、BE、AO、BO.则图中全等三角形的对数有科目:初中数学 来源: 题型:
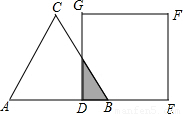
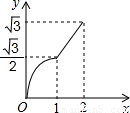
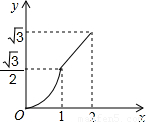
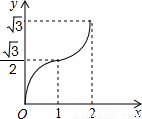
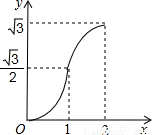
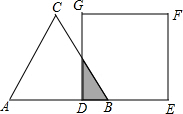 (2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
(2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )查看答案和解析>>
科目:初中数学 来源: 题型:
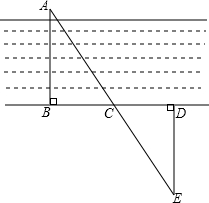 泰勒斯是古希腊哲学家,相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离.如图,B是观察点,船A在B的正前方,过B作AB的垂线,在垂线上截取任意长BD,C是BD的中点,观察者从点D沿垂直于BD的DE方向走,直到点E、船A和点C在一条直线上,那么△ABC≌△EDC,从而量出DE的距离即为船离岸的距离AB,这里判定△ABC≌△EDC的方法是( )
泰勒斯是古希腊哲学家,相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离.如图,B是观察点,船A在B的正前方,过B作AB的垂线,在垂线上截取任意长BD,C是BD的中点,观察者从点D沿垂直于BD的DE方向走,直到点E、船A和点C在一条直线上,那么△ABC≌△EDC,从而量出DE的距离即为船离岸的距离AB,这里判定△ABC≌△EDC的方法是( )查看答案和解析>>
科目:初中数学 来源:2012年10月中考数学模拟试卷(9)(解析版) 题型:选择题

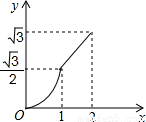
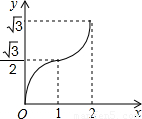
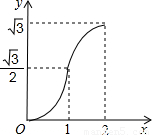
查看答案和解析>>
科目:初中数学 来源:2012年重庆市开县西街中学中考数学一模试卷(解析版) 题型:选择题
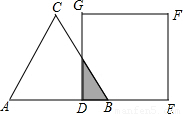
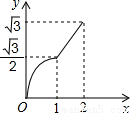
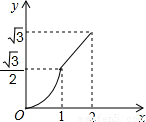
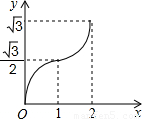
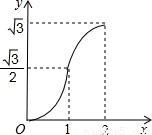
查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆市开县西街中学九年级模拟考试数学试卷(一)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com