
 (2012•江西二模)如图,BD、CF把矩形ABCD分成四块a、b、c、d,其中Sa=4,Sb=6,则Sc=?,Sd=?( )
(2012•江西二模)如图,BD、CF把矩形ABCD分成四块a、b、c、d,其中Sa=4,Sb=6,则Sc=?,Sd=?( )| EF |
| CE |
| 2 |
| 3 |
| S△DFE |
| S△BCE |
| EF |
| CE |
| S△DEF |
| S△DEC |
| EF |
| CE |
| 4 |
| 6 |
| EF |
| CE |
| 2 |
| 3 |
| S△DFE |
| S△BCE |
| EF |
| CE |
| 4 |
| 9 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
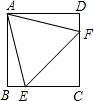 (2012•江西二模)如图,正方形ABCD中,点E、F分别在边BC、CD上,且AE=EF=FA.你能得出的结论是:(至少写两个)
(2012•江西二模)如图,正方形ABCD中,点E、F分别在边BC、CD上,且AE=EF=FA.你能得出的结论是:(至少写两个)查看答案和解析>>
科目:初中数学 来源:2009年重庆市梁平县云龙中学中考数学模拟试卷1(解析版) 题型:解答题
| 备选奖品 | 足球 | 篮球 | 排球 | 羽毛球拍 | 乒乓球拍 | 旱冰鞋 | 运动衫 | 象棋 | 围棋 |
| 单价(元) | 84 | 79 | 74 | 69 | 64 | 59 | 54 | 49 | 44 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com