
分析 因为三角形的高有三种情况,而直角三角形不合题意,故舍去,所以应该分两种情况进行分析,从而得到答案.
解答 解:当等腰三角形是锐角三角形时,如图1所示
∵CD⊥AB,CD=a,AC=2a,
∴sin∠A=$\frac{CD}{AC}$=$\frac{1}{2}$,
∴∠A=30°,
∴∠B=∠ACB=75°;
当等腰三角形是钝角三角形时,如图2示,
∵CD⊥AB,即在直角三角形ACD中,CD=a,AB=AC=2a,
∴sin∠CAD=$\frac{CD}{AC}$=$\frac{1}{2}$,
∴∠CAD=30°,
∴∠CAB=150°,
∴∠B=∠ACB=15°.
故其底角为15°或75°.
故答案为:15°或75°.
点评 此题主要考查等腰三角形的性质;在解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图所示,一次函数y1=ax+b的图象与反比例函数y2=$\frac{3}{x}$的图象相交于A,B两点,当y1>y2时,-1<x<0或x>3,则一次函数的解析式为y=x-2.
如图所示,一次函数y1=ax+b的图象与反比例函数y2=$\frac{3}{x}$的图象相交于A,B两点,当y1>y2时,-1<x<0或x>3,则一次函数的解析式为y=x-2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个相等的实数根 | B. | 有两个不等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
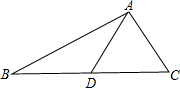 如图,AD是△ABC的中线,将△ABD绕点D旋转180°得到△ECD,若AB=15,AC=8,则:
如图,AD是△ABC的中线,将△ABD绕点D旋转180°得到△ECD,若AB=15,AC=8,则:查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省梅州市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
若a﹣b=3,则a2﹣2ab+b2﹣6的值是( )
A. 12 B. 6 C. 3 D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com