
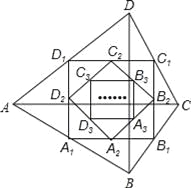
【题目】如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
【答案】B
【解析】试题分析:根据三角形的面积公式,可以求得四边形ABCD的面积是16;根据三角形的中位线定理,得A1B1∥AC,A1B1=A![]() C,则△BA1B1∽△BAC,得△BA1B1和△BAC的面积比是相似比的平方,即
C,则△BA1B1∽△BAC,得△BA1B1和△BAC的面积比是相似比的平方,即![]() ,因此四边形A1B1C1D1的面积是四边形ABCD的面积的
,因此四边形A1B1C1D1的面积是四边形ABCD的面积的![]() ,依此类推可得四边形AnBnCnDn的面积.
,依此类推可得四边形AnBnCnDn的面积.
∵四边形A1B1C1D1的四个顶点A1、B1、C1、D1分别为AB、BC、CD、DA的中点,
∴A1B1∥AC,A1B1=![]() AC, ∴△BA1B1∽△BAC, ∴△BA1B1和△BAC的面积比是相似比的平方,即
AC, ∴△BA1B1∽△BAC, ∴△BA1B1和△BAC的面积比是相似比的平方,即![]() ,
,
又四边形ABCD的对角线AC=8,BD=4,AC⊥BD, ∴四边形ABCD的面积是16,
∴SA1B1C1D1=![]() ×16, ∴四边形AnBnCnDn的面积=16×
×16, ∴四边形AnBnCnDn的面积=16×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】找规律:21-20=20 ;22-21=21 ;23-22=2 2;………利用你的发现,求20+21+22+23+…+22018+22019的值是( )
A. 22019 -1B. 22019 +1C. 22020 -1D. 22020 +1
查看答案和解析>>
科目:初中数学 来源: 题型:
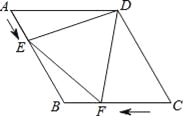
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )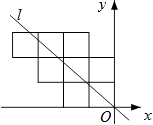
A.y=﹣x
B.y=﹣ ![]() x
x
C.y=﹣ ![]() x
x
D.y=﹣ ![]() x
x
查看答案和解析>>
科目:初中数学 来源: 题型:
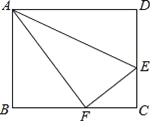
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10![]() cm,且tan∠EFC=
cm,且tan∠EFC=![]() ,那么该矩形的周长为_____.
,那么该矩形的周长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com