
| 售价x(元) | 60 | 70 | 80 | 90 | … |
| 销售量y(件) | 280 | 260 | 240 | 220 | … |
分析 (1)由x的值每增加10元时,y的值均减小20件知这个函数为一次函数,待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”列出函数解析式,再配方成顶点式依据二次函数的性质是解题的关键.
解答 解:(1)由表可知,x的值每增加10元时,y的值均减小20件,
据此可知y与x的函数关系为一次函数,
设该一次函数为y=k x+b,
代入(60,280)和(70,260),
得:$\left\{\begin{array}{l}{60k+b=280}\\{70k+b=260}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=400}\end{array}\right.$,
∴y=-2x+400,
将(80,240),(90,220)代入上式等式成立;
故答案为:一次函数.
(2)设月利润为w元,
则w=(x-40)y=(x-40)(-2x+400)=-2(x-120)2+12800,
∵-2<0,
∴当x=120时,w有最大值12800,
答:当售价定为120元时,利润最大,最大值为12800元.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法求函数解析式及根据相等关系列出函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
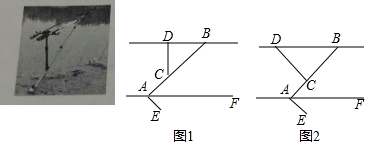
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
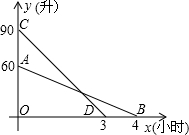 “滴滴出行”是一款涵盖出租车、专车、快车、顺风车等多项业务在内的一站式出行平台,如今已成为人们出行常用的“打车神器”,如图,分别是“滴滴出行”旗下甲、乙两辆轿车某天油箱中的剩余油量y(升)与行驶时间x(小时)的函数图象.
“滴滴出行”是一款涵盖出租车、专车、快车、顺风车等多项业务在内的一站式出行平台,如今已成为人们出行常用的“打车神器”,如图,分别是“滴滴出行”旗下甲、乙两辆轿车某天油箱中的剩余油量y(升)与行驶时间x(小时)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量P(件) | p=120-2x |
| 销售单价q(元/件) | 当1≤x<25时,q=x+60; 当25≤x≤50时,q=40+$\frac{1125}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
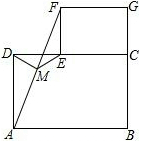 猜想与证明:
猜想与证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com