
【题目】如图所示,已知抛物线经过点 A (-2,0)、 B (4,0)、 C (0,-8),抛物线 y = a x 2 + b x + c (a≠0)与直线 y = x -4交于 B , D 两点.

(1)求抛物线的解析式并直接写出 D 点的坐标;
(2)点 P 为抛物线上的一个动点,且在直线 BD 下方,试求出△ BDP 面积的最大值及此时点 P 的坐标;
(3)点 Q 是线段 BD 上异于 B 、 D 的动点,过点 Q 作 QF ⊥ x 轴于点 F , 交抛物线于点 G . 当△ QDG 为直角三角形时,求点 Q 的坐标.
【答案】(1) (-1,-5);(2) (![]() ,-
,-![]() );(3) (2,-2)或 (3,-1)
);(3) (2,-2)或 (3,-1)
【解析】试题分析:(1)设抛物线的解析式为y=a(x+2)(x-4),将点C的坐标代入可求得a的值,然后将y=x-4与抛物线的解析式联立求解即可;
(2)过点P作PE∥y轴,交直线AB与点E,设P(x,x2-2x-8),则E(x,x-4),则PE═-x2+3x+4,然后依据S△BDP=S△DPE+S△BPE,列出△BDP的面积与x的函数关系式,然后依据二次函数的性质求解即可;
(3)设直线y=x-4与y轴相交于点K,则K(0,-4),设G点坐标为(x,x2-2x-8),点Q点坐标为(x,x-4),先证明△QDG为等腰直角三角形,然后根据
∠QDG=90°和∠DGQ=90°两种情况求解即可.
试题解析:(1)设抛物线的解析式为y=a(x+2)(x-4),将点C的坐标代入得:-8a=-8,解得:a=1,
∴抛物线的解析式为y=x2-2x-8.
将y=x-4代入抛物线的解析式得:x2-2x-8=x-4,解得:x=4或x=-1,
将x=-1代入y=x-4得:y=-5.
∴D(-1,-5).
(2)如图所示:
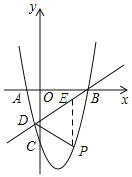
过点P作PE∥y轴,交直线AB与点E,设P(x,x2-2x-8),则E(x,x-4).
∴PE=x-4-(x2-2x-8)=-x2+3x+4.
∴S△BDP=S△DPE+S△BPE=![]() PE(xp-xD)+
PE(xp-xD)+![]() PE(xB-xE)=
PE(xB-xE)=![]() PE(xB-xD)=
PE(xB-xD)=![]() (-x2+3x+4)=-
(-x2+3x+4)=-![]() (x-
(x-![]() )2+
)2+![]() .
.
∴当x=![]() 时,△BDP的面积的最大值为
时,△BDP的面积的最大值为![]() .
.
∴P(![]() ,-
,-![]() ).
).
(3)设直线y=x-4与y轴相交于点K,则K(0,-4),设G点坐标为(x,x2-2x-8),点Q点坐标为(x,x-4).
∵B(4,0),
∴OB=OK=4.
∴∠OKB=∠OBK=45°.
∵QF⊥x轴,
∴∠DQG=45°.
若△QDG为直角三角形,则△QDG是等腰直角三角形.
①当∠QDG=90°时,过点D作
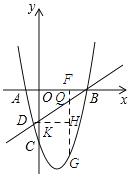
∴QG=2DH,QG=-x2+3x+4,DH=x+1,
∴-x2+3x+4=2(x+1),解得:x=-1(舍去)或x=2,
∴Q1(2,-2).
②当∠DGQ=90°,则DH=QH.
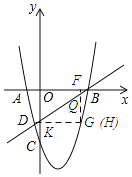
∴-x2+3x+4=x+1,解得x=-1(舍去)或x=3,
∴Q2(3,-1).
综上所述,当△QDG为直角三角形时,点Q的坐标为(2,-2)或(3,-1).


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的顶点为B(1,3),与
的顶点为B(1,3),与![]() 轴的交点A在点 (2,0)和(3,0)之间.以下结论:
轴的交点A在点 (2,0)和(3,0)之间.以下结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ≥
≥![]() ;⑤若
;⑤若![]() ,且
,且![]() ,
,
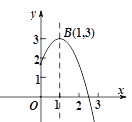
则![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为 ;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 2(2a 2 9b) 3(3a 2 4b)
(2)(![]() a 2 b2)(
a 2 b2)(![]() a b)(
a b)( ![]() a b)
a b)
(3) (![]() x 2y 3 )2 (3xy)3 (
x 2y 3 )2 (3xy)3 (![]() x 2 y 3)2 ( x)3 2 y 3
x 2 y 3)2 ( x)3 2 y 3
(4)用简便方法计算:9982 9980 16
查看答案和解析>>
科目:初中数学 来源: 题型:
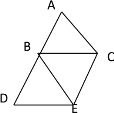
【题目】如图,等边三角形ABC沿边AB方向平移到△BDE的位置,则图中∠CBE=_____,连接CE后,线段CE与AD的关系是______,△BEC为____三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y﹣3与x成正比例,且x=2时,y=7.
(1)求出y与x之间的函数关系;
(2)画出函数的图象;
(3)结合所画出的图象直接写出当x满足什么条件时,函数的图象都在x轴的上方?
查看答案和解析>>
科目:初中数学 来源: 题型:
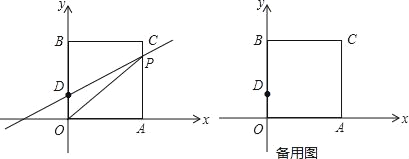
【题目】如图在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A,B分别在x,y轴上,已知OA=3,点D为y轴上一点,其坐标为(0,1),CD=5,点P从点A出发以每秒1个单位的速度沿线段A﹣C﹣B的方向运动,当点P与点B重合时停止运动,运动时间为t秒
(1)求B,C两点坐标;
(2)①求△OPD的面积S关于t的函数关系式;
②当点D关于OP的对称点E落在x轴上时,求点E的坐标;
(3)在(2)②情况下,直线OP上求一点F,使FE+FA最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 和一次函数
和一次函数![]() 的图象都经过点P(m,-3m).
的图象都经过点P(m,-3m).
(1)求点P的坐标和一次函数的解析式;
(2)若点M(a,y1)和点N(a+1,y2)(a>0)都在反比例函数的图象上,试通过计算或利用反比例的性质,说明y1与y2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com