
【题目】如图,已知:在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D , BC=CE . 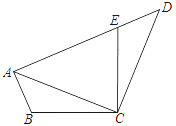
(1)求证:AC=CD;
(2)若AC=AE , 求∠DEC的度数.
【答案】
(1)解:证明:
![]()
![]()
![]()
在△ABC和△DEC中,  ,
,
![]()
![]()
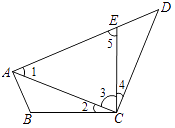
(2)解:∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°
【解析】(1)根据同角的余角相等得出∠ 2 = ∠ 4 , r然后利用AAS判断出ABC≌△DEC,再根据全等三角形的对应边相等得出结论;
(2)根据等腰直角三角形的性质知∠1=∠D=45°,又由知道顶角求等腰三角形底角的方法算出∠3=∠5=67.5°,利用邻补角的定义算出答案。
【考点精析】通过灵活运用等腰直角三角形和余角和补角的特征,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;互余、互补是指两个角的数量关系,与两个角的位置无关即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB的中点,分别以ED,EC为折痕将两个角,(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=4,BC=9,则EF的值是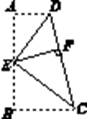
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为 . 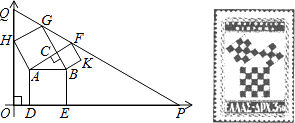
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为真命题的是( )
A.和为180°的两个角是邻补角B.内错角相等
C.经过直线外一点有且只有一条直线与这条直线平行D.同旁内角相等,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把长方形 ![]() 沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,
沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,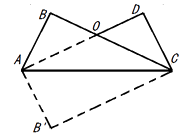
(1)求∠AOC和∠BAC的度数;
(2)若AD= ![]() ,OD=
,OD= ![]() ,求CD的长
,求CD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
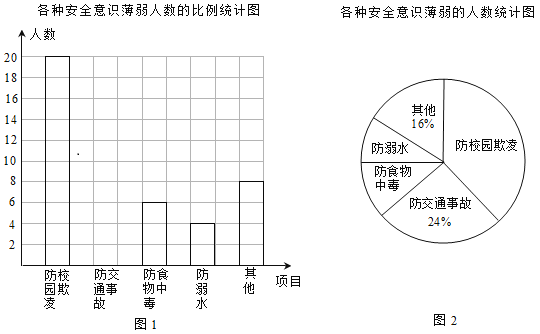
【题目】某校组织了一次防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识的调查活动,了解同学们在哪些方面的安全意识薄弱,便于今后更好地开展安全教育活动.根据调查结果,绘制出图1,图2两幅不完整的统计图.
请结合图中的信息解答下列问题:
(1)本次调查的人数为___________,其中防校园欺凌意识薄弱的人数占_________%;
(2)补全条形统计图;
(3)若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数;
(4)请你根据题中的信息,给该校的安全教育提一个合理的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com