
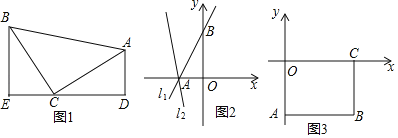
����Ŀ����ģ�ͽ�������1����ͼ1������ֱ��������ABC�У���ACB��90����CB��CA��ֱ��ED������C����A��AD��ED�ڵ�D����B��BE��ED�ڵ�E����֤����BEC�ա�CDA��
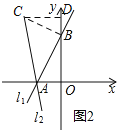
��ģ��Ӧ�ã���2������ֱ֪��l1��y��![]() x+3�������ύ�ڵ�A��B����ֱ��l1�Ƶ�A��ʱ����ת45o��ֱ��l2����ͼ2����ֱ��l2�ĺ�������ʽ��
x+3�������ύ�ڵ�A��B����ֱ��l1�Ƶ�A��ʱ����ת45o��ֱ��l2����ͼ2����ֱ��l2�ĺ�������ʽ��
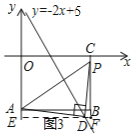
����ͼ3��������ABCO��OΪ����ԭ�㣬��B������Ϊ��8����6������A��C�ֱ����������ϣ���P���߶�BC�ϵĶ��㣬����APD���Ե�DΪֱ�Ƕ���ĵ���ֱ�������Σ�����D��ֱ��y����2x+5��ʱ��ֱ��д����D�����꣬��д�������˶������е�D��������n��ȡֵ��Χ��
���𰸡���1������������2����y����5x��10����D��3����1����![]() ����10��n����7��2��n��1��
����10��n����7��2��n��1��
��������
��1��������ABCΪ����ֱ�������Σ�AD��ED��BE��ED�����ж���ACD�ա�CBE��
��2���ٹ���B��BC��AB����l2��C����C��CD��y����D��������CBD�ա�BAO���ó�BD=AO=2��CD=OB=3�����C��-3��5����������ô���ϵ������ֱ��l2�ĺ�������ʽ��
�ڸ�����APD���Ե�DΪֱ�Ƕ���ĵ���ֱ�������Σ�����D��ֱ��y=-2x+5�ϵĶ������ڵ�������ʱ�����������������D�ھ���AOCB���ڲ�ʱ������D�ھ���AOCB���ⲿʱ����D��x��-2x+5�����ֱ������ADE�ա�DPF���ó�AE=DF���ݴ��г����̽�����⼴�ɣ��������������n�ķ�Χ���ɣ�
�⣺��1��֤������ͼ1���ߡ�ABCΪ����ֱ�������Σ�
��CB��CA����ACD+��BCE��90����
�֡�AD��ED��BE��ED��
���D����E��90������EBC+��BCE��90����
���ACD����EBC��
����ACD����CBE��
 ��
��
���ACD�ա�CBE��AAS����
��2������ͼ2������B��BC��AB����l2��C����C��CD��y����D��
�ߡ�BAC��45����
���ABCΪ����ֱ�������Σ�
�ɣ�1����֪����CBD�ա�BAO��
��BD��AO��CD��OB��
��ֱ��l1��y��![]() x+3�У���y��0����x����2����x��0����y��3��
x+3����y��0����x����2����x��0����y��3��
��A����2��0����B��0��3����
��BD��AO��2��CD��OB��3��
��OD��2+3��5��
��C����3��5����
��l2�Ľ���ʽΪy��kx+b����
![]() ��
��
��� ![]() ��
��
��l2�Ľ���ʽ��y����5x��10��
�ڵ���D��ֱ��y����2x+5�ϵĶ������ڵ�������ʱ�������������
����D�ھ���AOCB���ڲ�ʱ����ͼ�У���D��x���ƽ����EF����ֱ��OA��E����ֱ��BC��F��
��D��x����2x+5������OE��2x��5��AE��6����2x��5����11��2x��DF��EF��DE��8��x��
�ɣ�1���ɵã���ADE�ա�DPF����DF��AE��
����11��2x��8��x��
���x��3��
�ੁ2x+5����1��
��D��3����1����
��ʱ��PF��ED��3��CP��4��CB���������⣻
����D�ھ���AOCB���ⲿʱ����ͼ�У���D��x���ƽ����EF����ֱ��OA��E����ֱ��BC��F��
��D��x����2x+5������OE��2x��5��AE��OE��OA��2x��5��6��2x��11��DF��EF��DE��8��x��
ͬ���ɵã���ADE�ա�DPF����AE��DF��
����2x��11��8��x��
���x=![]() ��
��
��-2x+5=-![]() ��
��
��D�� ![]() ��-
��-![]() ����
����
��ʱ��ED=PF=![]() ��PB��6���������⣮
��PB��6���������⣮
�����������ĵ�D��3��-1����![]() ����
����
�ٵ���D��AP�·�ʱ����P��B�غ�ʱ��D��4����10������P��C�غ�ʱ��D��7����7����
�ੁ10��n����7��
�ڵ���D��AP�Ϸ�ʱ����P��B�غ�ʱ��D��4����2������P��C�غ�ʱ��D��1��1����
�ੁ2��n��1��
������������10��n����7��2��n��1��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵ���ֱ��������ABC�У���ACB=90�㣬AC=BC=4��D��AB���е㣬E��F�ֱ���AC��BC�ϵĵ㣨��E����˵�A��C�غϣ�����AE=CF.
��1����֤����ADE�ա�CDF
��2����ͼ2����EF��ȡEF���е�O������DO���ӳ�����G��ʹGO=OD������DE��DF��GE��GF����֤���ı���EDFG��������.
��3������E��ʲôλ��ʱ���ı���EDFG�������С��ֱ��д����E��λ�ü��ı���EDFG�������Сֵ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BE��CD�ֱ�Ϊ���ƽ�����ҽ��ڵ�O.
(1)����A��60��ʱ�����BOC�Ķ�����
(2)����A��100��ʱ�����BOC�Ķ�����
(3)����A����ʱ�����BOC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪƽ���ı������ӳ�AD��E��ʹDE=AD������EB��EC��DB������һ������������ʹ�ı���DBCE��Ϊ���ε����� ��

��A��AB=BE ��B��BE��DC ��C����ADB=90�� ��D��CE��DE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��
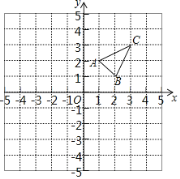
��1����������ABC����x��ԳƵ���A1B1C1��
��2������ABC����ƽ��4����λ���ȣ�����ƽ�ƺ����A2B2C2��
��3��������ͼ�������д��ڸ��P��ʹ��P�ĺᡢ������֮�͵��ڵ�C�ĺᡢ������֮�ͣ���д���������������ĸ��P�����꣨C���⣩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �������
�������![]() ·�����յ�
·�����յ�![]() ��
��![]() ���ٶ��˶���ͬʱ��
���ٶ��˶���ͬʱ��![]() ��
��![]() �������
�������![]() ·�����յ�
·�����յ�![]() ��
��![]() ���ٶ��˶������㶼Ҫ������Ӧ���յ�ʱ����ֹͣ�˶�.�ֱ��
���ٶ��˶������㶼Ҫ������Ӧ���յ�ʱ����ֹͣ�˶�.�ֱ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����˶�ʱ��
�����˶�ʱ��![]() ____________
____________![]() ʱ��
ʱ��![]() ��ȥ
��ȥ![]() ȫ�ȣ�
ȫ�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �����Σ�
������![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() �ӳ����ϣ�
�ӳ����ϣ�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() �ij�Ϊ
�ij�Ϊ![]() ��������
��������![]() �����Ϊ________��
�����Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����
����![]() ����
����![]() ���������Ľ�����
���������Ľ�����![]() ���·������н��ۣ���
���·������н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ���۵ĸ�����________����
��������ȷ���۵ĸ�����________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
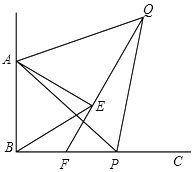
����Ŀ����ͼ����ABC=90��, PΪ����BC������һ��(��P�͵�B���غ�),�ֱ���AB,APΪ���ڡ�ABC�ڲ����ȱ���ABE�͵ȱ���APQ, ����QE���ӳ���BP�ڵ�F�� ��FQ=6, AB=2![]() ,��BP=__________
,��BP=__________
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com