
”¾ĢāÄæ”涞Ēą»įæŖÄ»Ź½ĘŚ¼ä£¬³ö×ā³µĖ¾»śĄīŹ¦øµÓŖŌĖŹ±ŹĒŌŚÄĻ±±×ßĻņµÄ±õŗÓĪ÷Ā·ÉĻŠŠ½ųµÄ£¬Čē¹ū¹ę¶ØĻņÄĻĪŖÕż£¬Ļņ±±ĪŖøŗ£¬ĖūÕāĢģÉĻĪēĖł½Ó![]() Ī»³ĖæĶµÄŠŠ³µĄļ³Ģ£Øµ„Ī»£ŗ
Ī»³ĖæĶµÄŠŠ³µĄļ³Ģ£Øµ„Ī»£ŗ![]() £©ĪŖ£ŗ
£©ĪŖ£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() .£Ø¼ŁÉčĻąĮŚĮ½Ī»³ĖæĶÉĻĻĀ³µĆ»ÓŠŹ±¼ä¼äøō£©
.£Ø¼ŁÉčĻąĮŚĮ½Ī»³ĖæĶÉĻĻĀ³µĆ»ÓŠŹ±¼ä¼äøō£©
£Ø1£©ŹŌÅŠ¶ĻĄīŹ¦øµ½«×īŗóŅ»Ī»³ĖæĶĖĶµ½ÄæµÄµŲŹ±£¬ĖūŌŚ³ö·¢µćµÄŹ²Ć“·½Ļņ£¬¾ąĄė³ö·¢µŲ¶ąÉŁĒ§Ć×£æ
£Ø2£©ČōĘū³µŗÄÓĶĮæĪŖ![]() £¬ŌņÕāĢģÉĻĪēĄīŹ¦øµ½ÓĖĶ³ĖæĶŹ±³ö×ā³µ¹²ŗÄÓĶ¶ąÉŁÉż£æ
£¬ŌņÕāĢģÉĻĪēĄīŹ¦øµ½ÓĖĶ³ĖæĶŹ±³ö×ā³µ¹²ŗÄÓĶ¶ąÉŁÉż£æ
£Ø3£©Čō³ö×ā³µĘš²½¼ŪĪŖ![]() ŌŖ£¬Ęš²½Ąļ³ĢĪŖ
ŌŖ£¬Ęš²½Ąļ³ĢĪŖ![]() £Ø°üĄØ
£Ø°üĄØ![]() £©,³¬¹ż²æ·ÖĆæĒ§Ć×
£©,³¬¹ż²æ·ÖĆæĒ§Ć×![]() ŌŖ£¬ĪŹĄīŹ¦øµÕāĢģÉĻĪē¹²µĆ³µ·Ń¶ąÉŁŌŖ£æ
ŌŖ£¬ĪŹĄīŹ¦øµÕāĢģÉĻĪē¹²µĆ³µ·Ń¶ąÉŁŌŖ£æ
”¾“š°ø”æ£Ø1£©½«×īŗóŅ»Ī»³ĖæĶĖĶµ½ÄæµÄµŲŹ±£¬ĄīŹ¦øµŌŚ³ö·¢µćŅŌ±±![]()
![]() µÄµŲ·½£»£Ø2£©ÕāĢģÉĻĪēĄīŹ¦øµ½ÓĖĶ³ĖæĶŹ±³ö×ā³µ¹²ŗÄÓĶ
µÄµŲ·½£»£Ø2£©ÕāĢģÉĻĪēĄīŹ¦øµ½ÓĖĶ³ĖæĶŹ±³ö×ā³µ¹²ŗÄÓĶ![]()
![]() £»£Ø3£©ĄīŹ¦øµÕāĢģÉĻĪē¹²µĆ³µ·Ń
£»£Ø3£©ĄīŹ¦øµÕāĢģÉĻĪē¹²µĆ³µ·Ń![]() ŌŖ
ŌŖ
”¾½āĪö”æ
£Ø1£©ĻČ½«Õā¼øøöŹżĻą¼Ó£¬ČōŗĶĪŖÕż£¬ŌņŌŚ³ö·¢µćµÄÄĻ±ß£¬ČōŗĶĪŖøŗ£¬ŌņŌŚ³ö·¢µćµÄ±±±ß£»£Ø2£©½«Õā¼øøöŹżµÄ¾ų¶ŌÖµĻą¼Ó£¬ŌŁ³ĖŅŌŗÄÓĶĮ漓æÉµĆ£»£Ø3£©²»³¬¹ż3Ē§Ć׵İ“8ŌŖ¼ĘĖć£¬³¬¹ż3Ē§Ć×µÄŌŚ8ŌŖµÄ»ł“”ÉĻ£¬ŌŁ¼ÓÉĻ³¬¹ż²æ·Ö³ĖŅŌ1.2ŌŖ¼“æɵĆ.
½ā£ŗ£Ø1£©![]() £¬
£¬
“š£ŗ½«×īŗóŅ»Ī»³ĖæĶĖĶµ½ÄæµÄµŲŹ±£¬ĄīŹ¦øµŌŚ³ö·¢µćŅŌ±±![]()
![]() µÄµŲ·½
µÄµŲ·½
£Ø2£©![]()
![]()
“š£ŗÕāĢģÉĻĪēĄīŹ¦øµ½ÓĖĶ³ĖæĶŹ±³ö×ā³µ¹²ŗÄÓĶ![]()
![]()
£Ø3£©![]() ŌŖ
ŌŖ
“š£ŗĄīŹ¦øµÕāĢģÉĻĪē¹²µĆ³µ·Ń![]() ŌŖ.
ŌŖ.


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
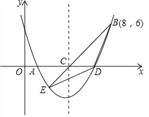
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży=![]() +bx+cµÄĶ¼Ļó½»xÖįÓŚA”¢DĮ½µć£¬²¢¾¹żBµć£¬ŅŃÖŖAµć×ų±źŹĒ£Ø2£¬0£©£¬BµćµÄ×ų±źŹĒ£Ø8£¬6£©£®
+bx+cµÄĶ¼Ļó½»xÖįÓŚA”¢DĮ½µć£¬²¢¾¹żBµć£¬ŅŃÖŖAµć×ų±źŹĒ£Ø2£¬0£©£¬BµćµÄ×ų±źŹĒ£Ø8£¬6£©£®
£Ø1£©Ē󶞓ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ĒóŗÆŹżĶ¼ĻóµÄ¶„µć×ų±ź¼°DµćµÄ×ų±ź£»
£Ø3£©øƶž“ĪŗÆŹżµÄ¶Ō³ĘÖį½»xÖįÓŚCµć£¬Į¬½ÓBC£¬²¢ŃÓ³¤BC½»Å×ĪļĻßÓŚEµć£¬Į¬½ÓBD”¢DE£¬Ēó”÷BDEµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚøų¶ØµÄĮ½øö”°ŗÆŹż£¬ČĪČ”×Ō±äĮæxµÄŅ»øöÖµ£¬µ±x<1Ź±£¬ĖüĆĒ¶ŌÓ¦µÄŗÆŹżÖµ»„ĪŖĻą·“Źż£»µ±x”Ż1Ź±£¬ĖüĆĒ¶ŌÓ¦µÄŗÆŹżÖµĻąµČ£¬ĪŅĆĒ³ĘÕāŃłµÄĮ½øöŗÆŹż»„ĪŖĻą¹ŲŗÆŹż.ĄżČē£ŗŅ»“ĪŗÆŹży=x-4£¬ĖüµÄĻą¹ŲŗÆŹżĪŖ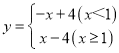 .
.
(1)Ņ»“ĪŗÆŹży= -x+5µÄĻą¹ŲŗÆŹżĪŖ______________.
(2)ŅŃÖŖµćA(b-1£¬4)£¬µćB×ų±ź(b+3£¬4)£¬ŗÆŹży=3x-2µÄĻą¹ŲŗÆŹżÓėĻ߶ĪABÓŠĒŅÖ»ÓŠŅ»øö½»µć£¬ĒóbµÄȔֵ·¶Ī§.
(3)µ±b+1”Üx”Üb+2Ź±£¬ŗÆŹży=-3x+b-2µÄĻą¹ŲŗÆŹżµÄ×īŠ”ÖµĪŖ3£¬ĒóbµÄÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDÄŚ½ÓÓŚ”ŃO£¬”ĻBAD=90”ć£¬¹żC×÷CE”ĶAD“¹×ćĪŖE£¬ĒŅ”ĻEDC=”ĻBDC.
£Ø1£©ĒóÖ¤:CEŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©ČōDE+CE=4£¬AB=6£¬ĒóBDµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬OĪŖ¾ŲŠĪABCD¶Ō½ĒĻߵĽ»µć£¬DE”ĪAC£¬CE”ĪBD£®

£Ø1£©ŹŌÅŠ¶ĻĖıߊĪOCEDµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ČōAB=6£¬BC=8£¬ĒóĖıߊĪOCEDµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ŅŃÖŖµćB£Ø8£¬0£©ŗĶµćC£Ø9£¬ ![]() £©£®Å×ĪļĻß
£©£®Å×ĪļĻß![]() £Øa£¬cŹĒ³£Źż£¬a”Ł0£©¾¹żµćB”¢C£¬ĒŅÓėxÖįµÄĮķŅ»½»µćĪŖA£®¶Ō³ĘÖįÉĻÓŠŅ»µćM £¬Āś×ćMA=MC£®
£Øa£¬cŹĒ³£Źż£¬a”Ł0£©¾¹żµćB”¢C£¬ĒŅÓėxÖįµÄĮķŅ»½»µćĪŖA£®¶Ō³ĘÖįÉĻÓŠŅ»µćM £¬Āś×ćMA=MC£®
£Ø1£©ĒóÕāĢõÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©ĒóĖıߊĪABCMµÄĆ껿£»
£Ø3£©Čē¹ū×ų±źĻµÄŚÓŠŅ»µćD£¬Āś×ćĖıߊĪABCDŹĒµČŃüĢŻŠĪ£¬ĒŅAD//BC£¬ĒóµćDµÄ×ų±ź£®
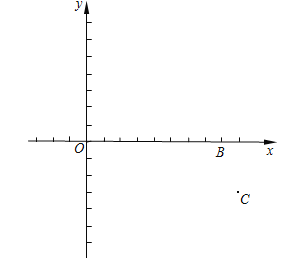
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÓɱ߳¤ĪŖ1øöµ„Ī»³¤¶ČµÄŠ”Õż·½ŠĪ×é³ÉµÄĶųøńÖŠ£¬øų³öĮĖøńµć”÷ABC(¶„µćŹĒĶųøńĻߵĽ»µćµÄČż½ĒŠĪ½ŠøńµćČż½ĒŠĪ)£¬
£Ø1£©Ēė»³ö”÷ABC¹ŲÓŚyÖį¶Ō³ĘµÄøńµć”÷A1B1C1£¬
£Ø2£©ĒėÅŠ¶Ļ”÷A1B1C1Óė”÷DEFŹĒ·ńĻąĖĘ£¬ČōĻąĖĘ£¬ĒėŠ“³öĻąĖĘ±Č£»Čō²»ĻąĖĘ£¬ĒėĖµĆ÷ĄķÓÉ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÕż·½ĢåµÄÕ¹æŖĶ¼ČēĶ¼ĖłŹ¾£¬Čē¹ūÕż·½ĢåµÄĮłøöĆę·Ö±šÓĆ×ÖÄøA£¬B£¬C£¬D£¬E£¬F±ķŹ¾£¬µ±ø÷ĆęÉĻµÄŹż·Ö±šÓėĖü¶ŌĆęµÄŹż»„ĪŖĻą·“Źż£¬ĒŅĀś×ćB=1£¬C=©a2©2a+1£¬D=©1£¬E=3a+4£¬F=2©aŹ±£¬ĒóAĆę±ķŹ¾µÄŹżÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży=©x+2µÄĶ¼ĻóÓė·“±ČĄżŗÆŹży=©![]() µÄĶ¼Ļó½»ÓŚA”¢BĮ½µć£¬ÓėxÖį½»ÓŚDµć£¬ĒŅC”¢DĮ½µć¹ŲÓŚyÖį¶Ō³Ę£®
µÄĶ¼Ļó½»ÓŚA”¢BĮ½µć£¬ÓėxÖį½»ÓŚDµć£¬ĒŅC”¢DĮ½µć¹ŲÓŚyÖį¶Ō³Ę£®
£Ø1£©ĒóA”¢BĮ½µćµÄ×ų±ź£»
£Ø2£©Ēó”÷ABCµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com