
【题目】如图(1), 点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() , 将一直角的直角项点放在点
, 将一直角的直角项点放在点![]() 处,即
处,即![]() 反向延长射线
反向延长射线![]() ,得到射线
,得到射线![]() .
.
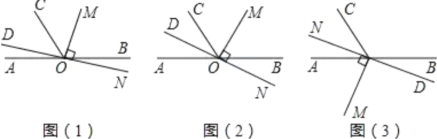
(1)当![]() 的位置如图(1)所示时,使
的位置如图(1)所示时,使![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
(2)当![]() 的位置如图(2)所示时,使一边
的位置如图(2)所示时,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,
,
问:射线![]() 的反向延长线
的反向延长线![]() 是否平分
是否平分![]() 请说明理由:注意:不能用问题
请说明理由:注意:不能用问题![]() 中的条件
中的条件
(3)当![]() 的位置如图
的位置如图![]() 所示时,射线
所示时,射线![]() 在
在![]() 的内部,若
的内部,若![]() .试探究
.试探究![]() 与
与![]() 之间的数量关系,不需要证明,直接写出结论.
之间的数量关系,不需要证明,直接写出结论.
【答案】![]() 为
为![]() ;
;![]() 平分
平分![]() ,理由见解析;
,理由见解析;![]()
【解析】
(1)∠NOB+∠BOC+∠COD=180°,根据题目已知条件代入即可求解;
(2) ∠MON=∠MOD=90°,利用互余的性质可以得出∠DOC=∠BON,由对顶角的性质得出∠BON=∠AOD,即可得出结果;
(3)根据∠BOC=120°,得出∠AOC=60°,再利用∠MON-∠AOC=30°即可得出结论.
解:(1)∵∠NOB=20°,∠BOC=120°
∠NOB+∠BOC+∠COD=180°
∴∠COD=180°-20°-120°=40°
(2)OD平分∠AOC
∵∠MON=∠MOD=90°
∴∠DOC+COM=∠MOB+∠BON
∵OM平分∠BOC
∴∠COM=∠MOB
∴∠DOC=∠BON
∵∠BON=∠AOD(对顶角相等)
∴∠AOD=∠DOC
∴OD平分∠AOC
(3)∵∠BOC=120°
∴∠AOC=180°-120°=60°
∵∠MON=90°
∴∠MON-∠AOC=30°
∴∠AOM+∠AON-∠AON-∠NOC=30°
∴∠AOM-∠NOC=30°


科目:初中数学 来源: 题型:
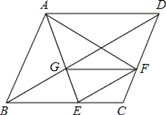
【题目】己知:如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
(1)求证:BE=DF;
(2)若![]() ,求证:四边形BEFG是平行四边形.
,求证:四边形BEFG是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与一次函数y=kx+5(k为常数,且k≠0)的图象交于A(﹣2,b),B两点.
的图象与一次函数y=kx+5(k为常数,且k≠0)的图象交于A(﹣2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是18,点E是AB边上的一个动点,点F是CD边上一点,![]() ,连接EF,把正方形ABCD沿EF折叠,使点A,D分别落在点
,连接EF,把正方形ABCD沿EF折叠,使点A,D分别落在点![]() ,
,![]() 处,当点
处,当点![]() 落在直线BC上时,线段AE的长为________.
落在直线BC上时,线段AE的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
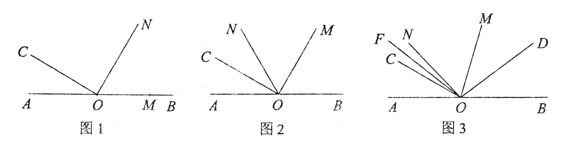
【题目】如图1, 点![]() 在直线
在直线![]() 上,
上,![]() ,将.
,将.![]() 绕着点
绕着点![]() 以
以![]() 的速度逆时针旋转,设旋转时间为
的速度逆时针旋转,设旋转时间为![]() .
.
(1)如图2,当![]() 平分
平分![]() 时,
时,![]() ______
______![]() ; 图中
; 图中![]() 的补角有: ______;
的补角有: ______;
(2)如图3,当![]() 时,
时,![]() 平分
平分![]() ,
, ![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
(3)在![]() 绕着点
绕着点![]() 逆时针旋转的过程中,当
逆时针旋转的过程中,当![]() ______
______![]() 时,
时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
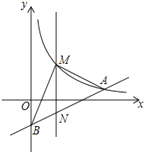
【题目】如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y=![]() (x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(1)k的值是______;
(2)当t=4时,求△BMN面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据国家实行的《国家学生体质健康标准》,对怀柔区初一学生身高进行抽样调查,以便总结怀柔区初一学生现存的身高问题,分析其影响因素,为学生的健康发展及学校体育教育改革提出合理项建议.已知怀柔区初一学生有男生840人,女生800人,他们的身高在150≤x<175范围内,随机抽取初一学生进行抽样调查.抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
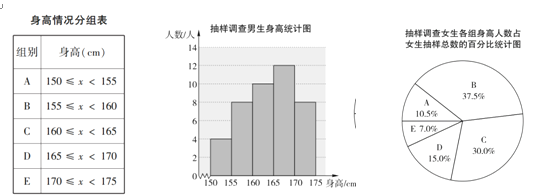
根据统计图表提供的信息,下列说法中
①抽取男生的样本中,身高在155≤x<165之间的学生有18人;
②初一学生中女生的身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④初一学生身高在160≤x<170之间的学生约有800人.
其中合理的是
A. ①② B. ①④ C. ②④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com