

���� ��1����OQ��Сʱ��Q��H�غϣ���ʱOQ=OH=4����O��Q�ľ������ʱ��O��P��Q���㹲�ߣ���ʱOQ=OP+PQ=5����O��P��Q���㹲��ʱ����Rt��OQH�У��ɹ��ɶ��������QH=3����ô��Q��l�ϵ��������Ϊ2QH=6��
��2����Ȼ���ԣ���Q��H�غ�ʱ��OP=2��PQ=3��OH=4����Ȼ������ֱ�������Σ���PQ���O�����У�
��3���ٵ�P��ֱ��l�ľ����ʱ�����������ΪPQ=3����ʱPQ��ֱ��l��
�ڵ�P��ֱ��l�ľ������ʱ��OP�������°ڶ��������P�ڶ�����������λ��ΪP��P�䣬����PP�䣬���ı���PQ��QP�Ǿ��Σ���OH��PP�佻�ڵ�D����ôPQ��=DH=PQ=3����OD=OH-DH=1����Rt��OPD�У�OP=2��OD=1�����POD=60�㣬��POP��=120�㣬�ɴ˵ý⣮
��� �⣺��1����OQ��Сʱ��Q��H�غϣ���ʱOQ=OH=4��
��O��Q�ľ������ʱ��O��P��Q���㹲�ߣ���ʱOQ=OP+PQ=5��
��O��P��Q���㹲��ʱ����Rt��OQH�У��ɹ��ɶ��������QH=3��
��ô��Q��l�ϵ��������Ϊ2QH=6��
�ʴ�Ϊ��4��5��6��
��2�����ԣ�
��OP=2��PQ=3��OH=4��
�ߵ�Q��H�غ�ʱ��OQ=OH=4��
��42��32+22����OQ2��PQ2+OP2��
��OP��PQ����ֱ����PQ���O�����У�
��3������ΪPQ��ֵ��Զ��3��ֻ��PQ��lʱ��
��P��ֱ��l�ľ������ʱ���ľ�����3���ף�
�ʴ�Ϊ��3��
���ɢ�֪���ڡ�O�ϴ��ڵ�P��P'��l�ľ���Ϊ3����ʱ��OP������������ת����
��ͼ��OP���Ƶ�O���Ұڶ���������ɨ����������ξ���P'OP��
����P'P����OH�ڵ�D��
��PQ��P'Q'����l��ֱ����PQ=P'Q'=3��
���ı���PQQ'P'�Ǿ��Σ�
��OH��PP'��PD=P'D��
��OP=2��OD=OH-HD=1���á�DOP=60�㣮
���POP'=120�㣮
���������Բ�ĽǵĶ���Ϊ120��
���� ������Բ���ۺ��⣬��Ҫ������Բ�����ʣ����ʵ�����⿼������ѧ���֪ʶ��Ӧ�ã��漰��֪ʶ���У����ɶ��������ߵ��ж������ε��ж������ʡ�������������Ҫ֪ʶ���Ȿ��Ĺؼ���֪��Բ��һ�㵽Բ�ϵĵ�����������С���룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ����̫���еڶ�ѧ�ڳ�һ����ģ����ѧ�Ծ��������棩 ���ͣ������
����ʽ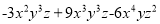 �Ĺ���ʽ��_________________��
�Ĺ���ʽ��_________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ���㽭ʡ���꼶3���¿���ѧ�Ծ��������棩 ���ͣ������
��ͼ��֪��AB��CD����1=45�㣬��2=80�㣬���3�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ���ı���OABC�Ǿ��Σ���D��OC���ϣ���ADΪ�ۺۣ�����OAD���Ϸ��ۣ���Oǡ������BC���ϵĵ�E��������ECD���ܳ�Ϊ4����EBA���ܳ�Ϊ12��
��ͼ��ʾ���ı���OABC�Ǿ��Σ���D��OC���ϣ���ADΪ�ۺۣ�����OAD���Ϸ��ۣ���Oǡ������BC���ϵĵ�E��������ECD���ܳ�Ϊ4����EBA���ܳ�Ϊ12���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
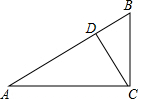 ��ͼ����Rt��ABC�У�CD��б��AB�ϵĸߣ���A��45�㣬�����б�ֵ�в�����sinA���ǣ�������
��ͼ����Rt��ABC�У�CD��б��AB�ϵĸߣ���A��45�㣬�����б�ֵ�в�����sinA���ǣ�������| A�� | $\frac{CD}{AC}$ | B�� | $\frac{CB}{AB}$ | C�� | $\frac{BD}{CB}$ | D�� | $\frac{CD}{CB}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
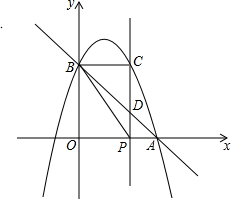 ��ͼ����֪������y=-x2+bx+c��x�������ύ�ڵ�A��3��0������y�ύ�ڵ�B��0��3������P��x����һ���㣬����P��x��Ĵ��߽��������ڵ�C����ֱ��AB�ڵ�D����P��x��0����
��ͼ����֪������y=-x2+bx+c��x�������ύ�ڵ�A��3��0������y�ύ�ڵ�B��0��3������P��x����һ���㣬����P��x��Ĵ��߽��������ڵ�C����ֱ��AB�ڵ�D����P��x��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com