
【题目】如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上.
(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1 . 在网格中画出△A1B1C1;
(2)求线段OA在旋转过程中扫过的图形面积;(结果保留π)
(3)求∠BCC1的正切值.
【答案】
(1)
解:如图.
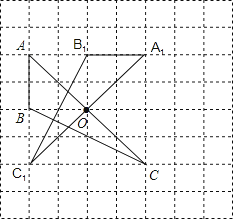
△A1B1C1即为所求三角形
(2)
解:由勾股定理可知OA= ![]() =2
=2 ![]() ,
,
线段OA在旋转过程中扫过的图形为以OA为半径,∠AOA1为圆心角的扇形,
则S扇形OAA1= ![]() =2π.
=2π.
答:扫过的图形面积为2π
(3)
解:在Rt△BCC1中,tan∠BCC1= ![]() =
= ![]() =
= ![]() .
.
答:∠BCC1的正切值是 ![]()
【解析】(1)根据图形旋转的性质画出旋转后的图形即可;(2)先根据勾股定理求出OA的长,再根据线段OA在旋转过程中扫过的图形为以OA为半径,∠AOA1为圆心角的扇形,利用扇形的面积公式得出结论即可;(3)直接根据锐角三角函数的定义即可得出结论.
【考点精析】利用扇形面积计算公式和锐角三角函数的定义对题目进行判断即可得到答案,需要熟知在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
(1)四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种圆盘,圆盘的半径x(cm),圆盘的售价y与x成正比例,圆盘的进价与x2成正比例,售出一个圆盘的利润是P(元).当x=10时,y=80,p=30.(利润=售价﹣进价).
(1)求y与x满足的函数关系式;
(2)求P与x满足的函数关系式;
(3)当售出一个圆盘所获得的利润是32元时,求这个圆盘的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,且
,且![]() 、
、![]() 满足
满足![]()
![]()
![]() 点
点![]() 表示的数为________;点
表示的数为________;点![]() 表示的数为________.
表示的数为________.
![]() 若点
若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数________.
点表示的数________.
![]() 若在原点
若在原点![]() 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点![]() 处以
处以![]() 个单位/秒的速度向左运动;同时另一小球乙从点
个单位/秒的速度向左运动;同时另一小球乙从点![]() 处以
处以![]() 个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为
个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为![]() (秒),请分别表示出甲、乙两小球到原点的距离(用含
(秒),请分别表示出甲、乙两小球到原点的距离(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
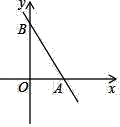
【题目】如图,直线y=﹣![]() x+4
x+4![]() 分别与x轴,y轴相交于点A,B,点C在直线AB上,D是坐标平面内一点,若以点O,A,C,D为顶点的四边形是菱形,则点D的坐标是_____.
分别与x轴,y轴相交于点A,B,点C在直线AB上,D是坐标平面内一点,若以点O,A,C,D为顶点的四边形是菱形,则点D的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型 | 运费 | |
运往甲地/(元/辆) | 运往乙地/(元/辆) | |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,延长弦BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.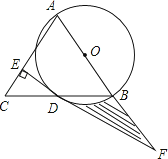
(1)判断直线DE与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为6,∠BAC=60°,延长ED交AB延长线于点F,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com