
【题目】如图,∠AOB是平角,射线OD平分∠AOC,射线OE平分∠BOD,且∠BOC=4∠AOD,求∠COE的度数. 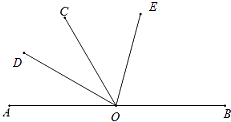
【答案】解:∵OD平分∠AOC,
∴∠AOD=∠COD= ![]() ∠AOC,
∠AOC,
∵∠BOC=4∠AOD,
∴∠BOC=2∠AOC,
∵∠BOC+∠AOC=180°,
∴3∠AOC=180°,
∴∠AOC=60°,
∴∠COD= ![]() ∠AOC=30°,∠BOC=2∠AOC=120°
∠AOC=30°,∠BOC=2∠AOC=120°
∴∠BOD=150°,
∵OE平分∠BOD,
∴∠EOD=∠BOE=75°,
∴∠COE=∠DOE﹣∠COD=75°﹣30°=45°
【解析】由OD平分∠AOC和∠BOC=4∠AOD,可求出∠AOC=60°,再求出∠COB的度数,即可求出∠BOD,利用∠COE=∠DOE﹣∠COD即可求出.
【考点精析】掌握角的平分线是解答本题的根本,需要知道从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
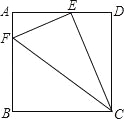
【题目】如图,在正方形ABCD中,E是AD的中点,F是AB边上一点,BF=3AF,则下列四个结论:
①△AEF∽△DCE;
②CE平分∠DCF;
③点B、C、E、F四个点在同一个圆上;
④直线EF是△DCE的外接圆的切线;
其中,正确的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二,产生新的微生物(依次被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么标号为1000的微生物会出现在( )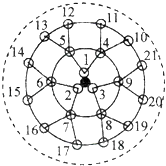
A.第7天
B.第8天
C.第9天
D.第10天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中约有红球个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB是直角,OE平分∠AOC,OF平分∠BOC. 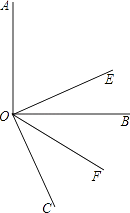
(1)若∠BOC=60°,求∠EOF的度数;
(2)若∠AOC=x°(x>90),此时能否求出∠EOF的大小,若能请求出它的数值;若不能,请用含x的代数式来表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②这六天中有4天空气质量为“优良”;③空气质量指数AQI与PM2.5浓度有关.其中正确的个数有( )
图(1)
图(2)
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com