



科目:初中数学 来源: 题型:
 9、如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入
9、如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•大庆)如图所示,将一个圆盘四等分,并把四个区域分别标上I、Ⅱ、Ⅲ、Ⅳ,只有区域I为感应区域,中心角为60°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
(2012•大庆)如图所示,将一个圆盘四等分,并把四个区域分别标上I、Ⅱ、Ⅲ、Ⅳ,只有区域I为感应区域,中心角为60°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )查看答案和解析>>
科目:初中数学 来源: 题型:
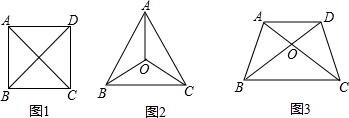
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
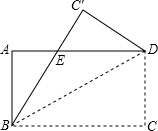 如图,在长方形纸片ABCD中,四个内角均为直角,AB=CD,AD=BC,将长方形纸片ABCD沿对角线BD进行折叠,点C的对称点为C′,BC′交AD于点E.
如图,在长方形纸片ABCD中,四个内角均为直角,AB=CD,AD=BC,将长方形纸片ABCD沿对角线BD进行折叠,点C的对称点为C′,BC′交AD于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com