
����Ŀ����ֱ������ϵxOy�У�ABCD�ĸ����������ֱ�ΪA��1��1����B��4��1����C��5��2����D��2��2����ֱ��l��y=kx+b��ֱ��y=��2xƽ�У�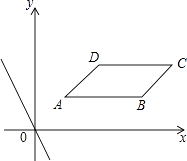
��1��k=��
��2����ֱ��l����D����ֱ��l�Ľ���ʽ��
��3����ֱ��lͬʱ���AB��CD���ཻ����b��ȡֵ��Χ��
��4����ֱ��l���߶�AC�ӵ�Aƽ������C����ֱ��l��x��Ľ���ΪP�����Ƿ����һ��P��ʹ��PABΪ���������Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��-2
��2���⣺��ֱ��l�Ľ���ʽ��y=��2x+b��
�ѣ�2��2������ã���4+b=2����ã�b=6��
��ֱ��l�Ľ���ʽ��y=��2x+6
��3���⣺���Aֱ��l�Ľ���ʽ��y=��2x+b���ѣ�1��1������ã���2+c=1����ã�c=3��
��ֱ�ߵĽ���ʽ��y=��2x+3��
ͬ������Cֱ��l�Ľ���ʽ��y=��2x+12��
��3��b��12
��4���⣺ 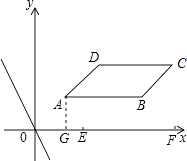
��ֱ��l����Aʱ������ʽ��y=��2x+3����y=0�����x= ![]() ������x��Ľ�����E��
������x��Ľ�����E�� ![]() ��0����
��0����
��ֱ��l����Cʱ������ʽ��y=��2x+12����y=0�����x=6������x��Ľ�����F��6��0����
��PA=PBʱ��P��AB���д����ϣ���P�������ǣ� ![]() ��0����
��0����
��AP=AB=3ʱ����PG= ![]() =2
=2 ![]() ����P�������ǣ�2
����P�������ǣ�2 ![]() +1��0����
+1��0����
ͬ������BP=BA=3ʱ��P�������ǣ�4��2 ![]() ��0����
��0����
��P�������ǣ��� ![]() ��0����2
��0����2 ![]() +1��0����4��2
+1��0����4��2 ![]() ��0����
��0����
����������1��������ֱ֪��l��y=kx+b��ֱ��y=��2xƽ�У�һ����ϵ����ͬ���ݴ˼�����á�
��2����ֱ��l�Ľ���ʽ��y=-2x+b����D������������ʽ�������b��ֵ�����ɵõ������Ľ���ʽ��
��3���ֱ���þ���A��C�Ľ���ʽ���������b��ȡֵ��Χ��
��4���ȷֱ������ֱ��l����Aʱ�͵�ֱ��l����Cʱ�ĺ�������ʽ���ٵ���PA=PB��AP=AB��BP=BA��������������ۼ�����⡣
�����㾫����������Ĺؼ���������ȷ��һ�κ����ı���ʽ�����֪ʶ������ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ�������Լ��Ե��������ε����ʵ����⣬�˽���������ε���������ȣ���ƣ��ȱ߶ԵȽǣ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=x2��2mx+m2+m��1��m�dz������Ķ���ΪP��ֱ��![]() ��y=x��1
��y=x��1
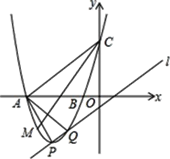
��1����֤����P��ֱ��![]() �ϣ�
�ϣ�
��2����m=��3ʱ����������x�ύ��A��B���㣬��y�ύ�ڵ�C����ֱ��![]() ����һ������ΪQ��M��x���·��������ϵ�һ�㣬��ACM=��PAQ����ͼ�������M�����ꣻ
����һ������ΪQ��M��x���·��������ϵ�һ�㣬��ACM=��PAQ����ͼ�������M�����ꣻ
��3�����������ߺ�ֱ��![]() ���������㼰����ԭ��Ϊ������������ǵ��������Σ���ֱ��д�����з���������m��ֵ��
���������㼰����ԭ��Ϊ������������ǵ��������Σ���ֱ��д�����з���������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��l��һ��P��ֱ��l����������߶γ��ֱ�Ϊ3cm��5cm�����P��ֱ��l�ľ����ǣ�������
A. ������3cmB. 3cmC. 5cmD. ������5cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ������ġ�һ��һ·�����轫�ٽ��ҹ�����������Ļ�����������һ��һ·�������������˿�ԼΪ4400000000�ˣ�������4400000000�ÿ�ѧ��������ʾΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BC=EC����BCE=��ACD�������Ӳ���ʹ��ABC�ա�DBC�������ǣ� ��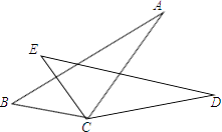
A.AB=DE
B.��B=��E
C.AC=DC
D.��A=��D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��һ64����������b������ƽ����Ϊ2.
(1)д��a��b��ֵ;
(2)��3bһa��ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��0�� ![]() ��ΪԲ�ĵ�Բ��x������������ԭ��O����y���ཻ�ڵ�B����BD���ӳ��߽�x��ĸ������ڵ�E���ҡ�BEO��60�㣬AD���ӳ��߽�x���ڵ�C��
��ΪԲ�ĵ�Բ��x������������ԭ��O����y���ཻ�ڵ�B����BD���ӳ��߽�x��ĸ������ڵ�E���ҡ�BEO��60�㣬AD���ӳ��߽�x���ڵ�C��
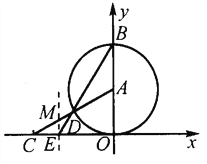
��1���ֱ����E��C�����ꣻ
��2����A��C���㣬���Թ�E��ƽ����y���ֱ��Ϊ�Գ���������ߵĺ�������ʽ��
��3���������ߵĶԳ�����AC�Ľ���ΪM�����ж���M��ΪԲ�ģ�MEΪ�뾶��Բ���A��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й��˺��翪ʼʹ�ø������й��Ŵ���ѧ�����������������ġ����̡�һ�£���������ѧʷ���״���ʽ���븺�����������100Ԫ����+100Ԫ����ô��80Ԫ��ʾ�� ��
A.֧��20Ԫ
B.����20Ԫ
C.֧��80Ԫ
D.����80Ԫ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com