
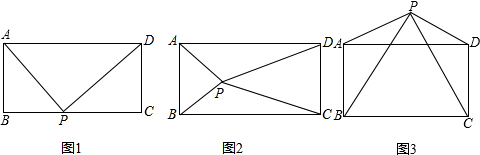
���� ��1��ֱ�Ӹ��ݹ��ɶ������ɵó����ۣ�
��2������P��MN��AD�ڵ�M����BC�ڵ�N������Rt��AMP��Rt��BNP��Rt��DMP��Rt��CNP�ֱ��ù��ɶ�����ʾ��PA2��PC2��PB2��PD2��Ȼ�����ǿɵó�PA2+PC2��PB2+PD2�����Dz��ѵó��ı���MNCD�Ǿ��Σ����ǣ�MD=NC��AM=BN��Ȼ�����ǽ���ʽ�ұߵ�ֵ���бȽϷ���PA2+PC2=PB2+PD2����ͼ��3������ͬ��2��������P��PQ��BC��AD��BC��O����֤��
��� ֤������1����ͼ1�У�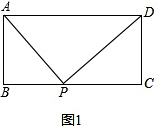
��Rt��ABP��AB2=AP2-BP2��Rt��PDC��CD2=PD2-PC2��
��AB=CD��
��AP2-BP2=PD2-PC2��
��PA2+PC2=PB2+PD2��
��2�����룺PA2+PC2=PB2+PD2��
��ͼ2������P��MN��AD�ڵ�M����BC�ڵ�N��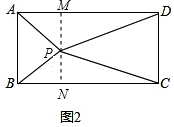
���ھ���ABCD�У�AD��BC��MN��AD��
��MN��BC��
����Rt��AMP��PA2=PM2+MA2����Rt��BNP��PB2=PN2+BN2��
��Rt��DMP��PD2=DM2+PM2����Rt��CNP��PC2=PN2+NC2��
��PA2+PC2=PM2+MA2+PN2+NC2��
PB2+PD2=PM2+DM2+BN2+PN2��
��MN��AD��MN��NC��DC��BC��
���ı���MNCD�Ǿ��Σ�
��MD=NC��ͬ��AM=BN��
��PM2+MA2+PN2+NC2=PM2+DM2+BN2+PN2����PA2+PC2=PB2+PD2��
��3����ͼ3������P��PQ��BC��AD��BC��O��Q��
���ھ���ABCD�У�AD��BC��PQ��BC��
��PQ��AD��
����Rt��AOP��PA2=AO2+PO2����Rt��PQB��PB2=PQ2+QB2��
��Rt��POD��PD2=DO2+PO2����Rt��CQP��PC2=PQ2+QC2��
��PA2+PC2=PO2+OA2+PQ2+QC2��
PB2+PD2=PQ2+QB2+DO2+PO2��
��PQ��AD��PQ��NC��DC��BC��
���ı���OQCD�Ǿ��Σ�
��OD=QC��ͬ��AO=BQ��
��PA2+PC2=PB2+PD2��
���� ���⿼����ε����ʡ����ɶ�����֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ֱ�������ν�����⣬�����п��������ͣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
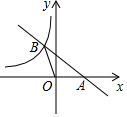 ��ͼ��ֱ��y=-$\frac{1}{2}$x+b��x�ύ�ڵ�A����˫����y=-$\frac{4}{x}$��x��0�����ڵ�B����S��AOB=2����b��ֵ�ǣ�������
��ͼ��ֱ��y=-$\frac{1}{2}$x+b��x�ύ�ڵ�A����˫����y=-$\frac{4}{x}$��x��0�����ڵ�B����S��AOB=2����b��ֵ�ǣ�������| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
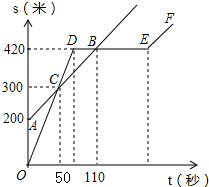 ij��ѧ��С��������ʦһ��һ����ֱ���ܵ��϶������壬��������С������һ���������ʦ���ܣ���С������ʱ������ʦ�Ѿ������200���ˣ����Ǿ����ľ���s���ף���С��������ʱ��t���룩֮��Ĺ�ϵ��ͼ��ʾ����������������ͼ�и�������Ϣ������������⣺
ij��ѧ��С��������ʦһ��һ����ֱ���ܵ��϶������壬��������С������һ���������ʦ���ܣ���С������ʱ������ʦ�Ѿ������200���ˣ����Ǿ����ľ���s���ף���С��������ʱ��t���룩֮��Ĺ�ϵ��ͼ��ʾ����������������ͼ�и�������Ϣ������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
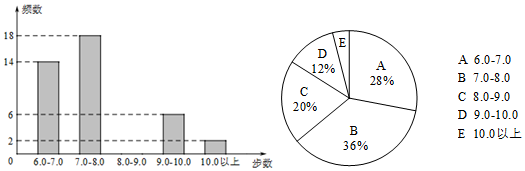
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �༶ | ��߷� | ƽ���� | ��λ�� | ���� | ���� |
| �ţ�1���� | 100 | 94 | b | 93 | 12 |
| �ţ�2���� | 99 | a | 95.5 | 93 | 8.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
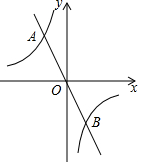 ��ͼ����ƽ��ֱ������ϵ�У���A�ǵڶ�������˫����y=-$\frac{2}{x}$��һ�㣬ֱ��AO��˫���ߵ���һ������ΪB��
��ͼ����ƽ��ֱ������ϵ�У���A�ǵڶ�������˫����y=-$\frac{2}{x}$��һ�㣬ֱ��AO��˫���ߵ���һ������ΪB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com