
【题目】如图所示,点P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列四个结论:①AP=EF;②△APD一定是等腰三角形;③∠PFE=∠BAP;④PD=![]() EC,其中正确结论的序号是_______.
EC,其中正确结论的序号是_______.
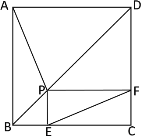
【答案】①③④.
【解析】
连接PC,根据正方形的对角线平分一组对角可得∠ABP=∠CBP=45°,然后利用“边角边”证明△ABP和△CBP全等,根据全等三角形对应边相等可得AP=PC,对应角相等可得∠BAP=∠BCP,再根据矩形的对角线相等可得EF=PC,对边相等可得PF=EC,再判断出△PDF是等腰直角三角形,然后根据等腰直角三角形的斜边等于直角边的![]() 倍解答即可.
倍解答即可.
解:如图,连接PC,在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
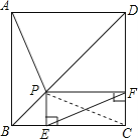
∵在△ABP和△CBP中,
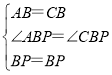 ,
,
∴△ABP≌△CBP(SAS),
∴AP=PC,∠BAP=∠BCP,
又∵PE⊥BC,PF⊥CD,
∴四边形PECF是矩形,
∴PC=EF,∠BCP=∠PFE,
∴AP=EF,∠PFE=∠BAP,故①③正确;
∵PF⊥CD,∠BDC=45°,
∴△PDF是等腰直角三角形,
∴PD=![]() PF,
PF,
又∵矩形的对边PF=EC,
∴PD=EC,故④正确;
只有点P为BD的中点或PD=AD时,△APD是等腰三角形,故②错误;
综上所述,正确的结论有①③④.
故答案为:①③④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:

(1)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为![]() ,且点B在格点上;
,且点B在格点上;
(2)以上题中所画线段AB为一边,另外两条边长分别是3,![]() ,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);
,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);
(3)所画的三角形ABC的AB边上高线长为_________(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区积极响应正在开展的“创文活动”,组织甲、乙两个志愿工程队对社区的一些区域进行绿化改造.已知甲工程队每小时能完成的绿化面积是乙工程队每小时能完成的绿化面积的2倍,并且甲工程队完成300平方米的绿化面积比乙工程队完成300平方米的绿化面积少用3小时,乙工程队每小时能完成多少平方米的绿化面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.

(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
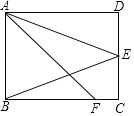
【题目】如图,在平行四边形ABCD中,点E是CD的中点,点F是BC边上的点,AF=AD+FC,平行四边形ABCD的面积为S,由A、E、F三点确定的圆的周长为t.
(1)若△ABE的面积为30,直接写出S的值;
(2)求证:AE平分∠DAF;
(3)若AE=BE,AB=4,AD=5,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,他在封闭图形内划出了一个半径为1米的圆,在不远处向图形内掷石子,且记录如下:

(1)随着次数的增多,小明发现m与n的比值在一个常数k附近波动,请你写出k的值。
(2)请利用学过的知识求出封闭图形ABC的大致面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七(1)班学生为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题;
级别 | A | B | C | D | E | F |
月均用水量x(t) | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | 20<x≤25 | 25<x≤30 |
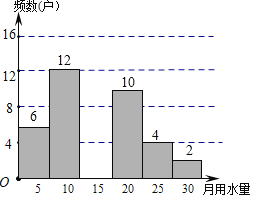
频数(户) | 6 | 12 | m | 10 | 4 | 2 |
(1)本次调查采用的方式是 (填“全面调查”或“抽样调查);
(2)若将月均用水量的频数绘成形统计图,月均用水量“15<x≤20”组对应的圆心角度数是72°,则本次调查的样本容量是 ,表格中m的值是 ,补全频数分布直方图.
(3)该小区有500户家庭,求该小区月均用水量超过15t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
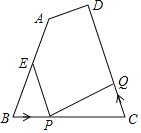
【题目】如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com