
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
(1)证明见解析;(2)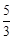 或6.
或6.
解析试题分析:(1)由两对角相等(∠APQ=∠C,∠A=∠A),证明△APQ∽△ABC;(2)当△PQB为等腰三角形时,有两种情况,需要分类讨论:(I)当点P在线段AB上时,如题图1所示,由△APQ∽△ABC计算AP的长,(II)当点P在线段AB的延长线上时,如题图2所示,利用角之间的关系,证明点B为线段AP的中点,从而可以求出AP.
试题解析:(1)∵∠A+∠APQ=90°,∠A+∠C=90°,∴∠APQ=∠C.
在△APQ与△ABC中,∵∠APQ=∠C,∠A=∠A,∴△APQ∽△ABC.
(2)在Rt△ABC中,AB=3,BC=4,由勾股定理得:AC=5.
∵∠BPQ为钝角,∴当△PQB为等腰三角形时,只可能是PB=PQ.
(I)当点P在线段AB上时,如题图1所示,
由(1)可知,△APQ∽△ABC,∴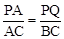 ,即
,即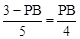 ,解得:
,解得: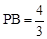 .
.
∴ .
.
(II)当点P在线段AB的延长线上时,如题图2所示,
∵BP=BQ,∴∠BQP=∠P.
∵∠BQP+∠AQB=90°,∠A+∠P=90°,∴∠AQB=∠A. ∴BQ=AB.
∴AB=BP,点B为线段AB中点.
∴AP=2AB=2×3=6.
综上所述,当△PQB为等腰三角形时,AP的长为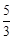 或6.
或6.
考点:1.相似三角形的判定和性质;2.勾股定理;3.等腰三角形的性质;4.直角三角形斜边上中线的性质;5.分类思想的应用.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
老师要求同学们在图①中 内找一点P,使点P到OM、ON的距离相等.
内找一点P,使点P到OM、ON的距离相等.
小明是这样做的:在OM、ON上分别截取OA=OB,连结AB,取AB中点P,点P即为所求.
请你在图②中的 内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.
内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米.求路灯的高.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡角 为
为 ,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为500米.
,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为500米.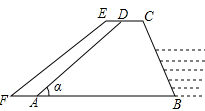
(1)求完成该工程需要多少立方米方土?
(2)某工程队在加固600立方米土后,采用新的加固模式,这样每天加固方数是原来的2倍,结果只用11天完成了大坝加固的任务.请你求出该工程队原来每天加固多少立方米土?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上一点(不与点A、B重合),连结CO并延长CO交⊙O于点D,连结AD.
(1)求弦长AB的长度;(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE ,CF
,CF .
.
图1
(1)求 关于
关于 的函数解析式,并写出
的函数解析式,并写出 的取值范围;
的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证: ;
;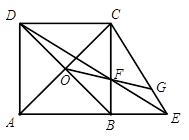
图2
(3)在(2)的条件下,当 时,求
时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
(1)当PE⊥AB,PF⊥BC时,如图1,则 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3, 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com