
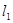 为
为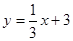 与直线
与直线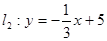 相交于A点,直线
相交于A点,直线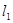 交
交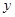 轴于B点,直线
轴于B点,直线 交
交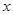 轴于C点,求 ① A点的坐标; ② △ABC的面积。
轴于C点,求 ① A点的坐标; ② △ABC的面积。
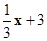 与直线l2:y=-
与直线l2:y=-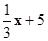 的交点
的交点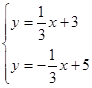 可得:x=3,y=4
可得:x=3,y=4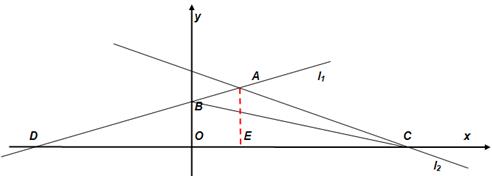
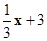 ,令x=0得:y=3;令y=0得:x=-9
,令x=0得:y=3;令y=0得:x=-9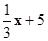 ,令y=0得:x=15
,令y=0得:x=15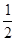 (OD+OC)·AE=
(OD+OC)·AE=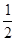 ×(9+15)×4=48
×(9+15)×4=48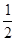 (OD+OC)·OB=
(OD+OC)·OB=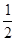 ×(9+15)×3=36
×(9+15)×3=36

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源:不详 题型:单选题
| A.70°,70° | B. 70°,70°或40°,100° |
| C.40°,40° | D. 40°,70° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、线段AB及射线OM,按下列要求画图:
、线段AB及射线OM,按下列要求画图:


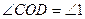 ;
;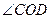 的边OD上取一点E,使OE=2AB;
的边OD上取一点E,使OE=2AB;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
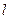 同侧,在直线
同侧,在直线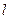 上找一点P,使AP+BP的值最小.
上找一点P,使AP+BP的值最小.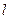 的对称点
的对称点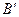 ,连接
,连接 ,与直线
,与直线 的交点就是所求的点P
的交点就是所求的点P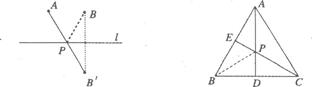
 的中点,在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.
的中点,在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.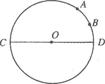
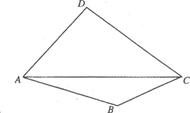
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com