
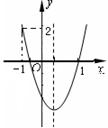
如图,二次函数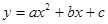 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与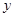 轴交于负半轴.给出四个结论:①abc<0;②2a+
轴交于负半轴.给出四个结论:①abc<0;②2a+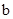 >0;③a+c=1; ④a>1.其中正确结论的序号是 (将你认为正确结论的序号都填上)
.
>0;③a+c=1; ④a>1.其中正确结论的序号是 (将你认为正确结论的序号都填上)
.
②,③,④
【解析】
试题分析:如图,二次函数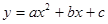 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与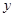 轴交于负半轴,令x=0,得y=
轴交于负半轴,令x=0,得y=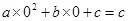 〈0,观察图形二次函数的开口方向向上,所以a〉0,其对称轴为于y轴的右边,所以
〈0,观察图形二次函数的开口方向向上,所以a〉0,其对称轴为于y轴的右边,所以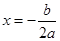 >0,所以b<0,所以abc>0,所以①错误;二次函数
>0,所以b<0,所以abc>0,所以①错误;二次函数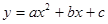 的图象开口向上,图象经过点(-1,2)和(1,0),所以a-b+c=2,a+b+c=0,两式子相加得2a+2c=2,所以a+c=1,因此③正确;a-b+c=2,a+b+c=0,两式子相减得b=-1;由图象可观察出0<
的图象开口向上,图象经过点(-1,2)和(1,0),所以a-b+c=2,a+b+c=0,两式子相加得2a+2c=2,所以a+c=1,因此③正确;a-b+c=2,a+b+c=0,两式子相减得b=-1;由图象可观察出0<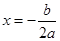 <1,又因为b=-1,所以
<1,又因为b=-1,所以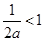 ,解得a>1,所以④正确;因为c<0, a+b+c=0,所以a+b>0,又因为a>0,所以2a+
,解得a>1,所以④正确;因为c<0, a+b+c=0,所以a+b>0,又因为a>0,所以2a+ >0,因此②正确,所以正确结论的序号有②,③,④
>0,因此②正确,所以正确结论的序号有②,③,④
考点:二次函数
点评:本题考查抛物线,解答本题需要考生掌握抛物线的性质,比如求其顶点坐标,对称轴,与坐标轴的交点,开口方向,二次函数是中考的重点


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京市华夏女子中学九年级第一学期期中考试数学卷 题型:解答题
如图是二次函数 的图象,其顶点坐标为M(1,-4).
的图象,其顶点坐标为M(1,-4).
【小题1】(1)求出图象与 轴的交点A,B的坐标;
轴的交点A,B的坐标;
【小题2】(2)在二次函数的图象上是否存在点P,使 ,若存在,求出P点的坐标;若不存在,请说明理由;
,若存在,求出P点的坐标;若不存在,请说明理由;
【小题3】(3)将二次函数的图象在 轴下方的部分沿
轴下方的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线 与此图象有两个公共点时,
与此图象有两个公共点时, 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2013年上海市中考数学模拟试卷(二)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年上海市浦东新区中考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com