
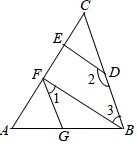
 如图,DE⊥AC,∠AGF=ABC,∠1+∠2=180°,
如图,DE⊥AC,∠AGF=ABC,∠1+∠2=180°,分析 (1)根据平行线的判定,可得BC∥GF,进而得出∠1=∠3,再根据∠1+∠2=180°,可得BF∥DE,最后根据DE⊥AC,可得BF⊥AC.
(2)根据∠1+∠2=180°,∠2=150°,可得∠1=30°,再根据BF⊥AC,即可得出∠AFB=90°,进而得到∠AFG=90°-∠1=60°.
解答 解:(1)BF与AC的位置关系是:BF⊥AC.
理由:∵∠AGF=∠ABC,
∴BC∥GF,
∴∠1=∠3,
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE,
∵DE⊥AC,
∴BF⊥AC.
(2)∵∠1+∠2=180°,∠2=150°,
∴∠1=30°,
又∵BF⊥AC,
∴∠AFB=90°,
∴∠AFG=90°-∠1=60°.
点评 本题主要考查了平行线的性质与判定的运用,解题时注意:同位角相等,两直线平行;两直线平行,内错角相等.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
 高考英语听力测试期间,需要杜绝考点周围的噪音,如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C处有一消防队,在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火.已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改进行驶,试问:消防车是否需要改道行驶?请说明理由.
高考英语听力测试期间,需要杜绝考点周围的噪音,如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C处有一消防队,在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火.已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改进行驶,试问:消防车是否需要改道行驶?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com