
����Ŀ����֪����ͼ����Rt��ABC�У���C=90������A=30����BC=18cm������P�ӵ�A��������AB���B�˶�������Q�ӵ�B��������BC���C�˶����������P��2cm/s��Q��1cm/s���ٶ�ͬʱ���������˶�ʱ��Ϊt(s)������������⣺
(1)tΪ______ʱ����PBQ�ǵȱ������Σ�
(2)P��Q���˶������У���PBQ����״���Ϸ����仯����tΪ��ֵʱ����PBQ��ֱ�������Σ�˵�����ɣ�

���𰸡�(1)12��(2)��tΪ9��![]() ʱ����PBQ��ֱ�������Σ����ɼ�����.
ʱ����PBQ��ֱ�������Σ����ɼ�����.
��������
��1�����ݵȱ������ε����ʽ�ɣ�
��2���������������ֱ�������ε����ʽ�ɣ�
(1)Ҫʹ����PBQ�ǵȱ������Σ����ɵã�PB=BQ��
����Rt��ABC����C=90������A=30����BC=18cm��
��AB=36cm��
�ɵã�PB=36-2t��BQ=t��
��36-2t=t��
��ã�t=12
�ʴ�Ϊ��12
(2)��tΪ9��![]() ʱ����PBQ��ֱ�������Σ�
ʱ����PBQ��ֱ�������Σ�
�������£�
�ߡ�C=90������A=30����BC=18cm
��AB=2BC=18��2=36(cm)
������P��2cm/s��Q��1cm/s���ٶȳ���
��BP=AB-AP=36-2t��BQ=t
�ߡ�PBQ��ֱ��������
��BP=2BQ��BQ=2BP
��BP=2BQʱ��
36-2t=2t
���t=9
��BQ=2BPʱ��
t=2(36-2t)
���t=![]()
���ԣ���tΪ9��![]() ʱ����PBQ��ֱ�������Σ�
ʱ����PBQ��ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=4cm����ADC=120������E��Fͬʱ��A��C����������ֱ���AB��CB�������B�����ƶ�������BΪֹ������E���ٶ�Ϊ1cm/s����F���ٶ�Ϊ2cm/s������t����DEFΪ�ȱ������Σ���t��ֵΪ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���![]() ���������㣺
���������㣺![]()
��1�������![]() ������
������
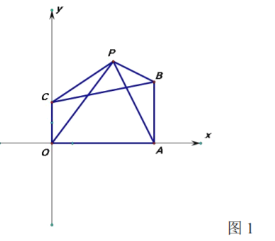
��2����ͼ1������![]() ����
����![]() ���ı���
���ı���![]() �������ڵ�һ���ޣ�����
�������ڵ�һ���ޣ�����![]() ����
����![]() ����
����![]() �����꣮
�����꣮
��3����ͼ2��ʾ��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬
��һ���㣬![]() ����
����![]() �ҲࣩΪ
�ҲࣩΪ![]() ��һ���㣬ʹ
��һ���㣬ʹ![]() ��ʼ��ƽ��
��ʼ��ƽ��![]() ����
����![]() ��
��![]() ����ô
����ô![]() �Ƿ�Ϊ��ֵ����Ϊ��ֵ����ֱ��д����ֵ�������ǣ����˵�����ɣ�
�Ƿ�Ϊ��ֵ����Ϊ��ֵ����ֱ��д����ֵ�������ǣ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��ѧϰ��ȫ�������ε����֪ʶ���֣�ֻ��������ȫ��ͬ�ij�����ֱ�߾Ϳ�������һ���ǵ�ƽ���ߣ���ͼ��һ��ֱ��ѹס����OB����һ��ֱ��ѹס����OA�������һ��ֱ�߽��ڵ�P��С��˵��������OP���ǡ�BOA�Ľ�ƽ���ߣ�������������������(����)

A. �ǵ��ڲ����ǵ����ߵľ�����ȵĵ��ڽǵ�ƽ������
B. ��ƽ�����ϵĵ㵽��������ߵľ������
C. ������������ƽ���ߵĽ��㵽�����ߵľ������
D. ���Ͼ�����ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������֤����
��֪����ͼ���� D��E��F �ֱ����߶� AB��BC��AC �ϣ����� DE��EF��DM ƽ�֡�ADE �� EF �ڵ� M����1+��2=180���� ��֤����B =��BED��
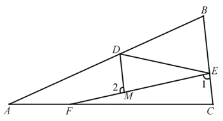
֤�����ߡ�1+��2=180������֪����
���ߡ�1+��BEM=180����ƽ�Ƕ��壩��
���2=��BEM�� ����
��DM�� �� ����
���ADM =��B�� ����
��MDE =��BED�� ����
����DM ƽ����ADE (��֪)��
���ADM =��MDE (��ƽ���߶���)��
���B =��BED�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ӻ�����ʶ��ij�����ƻ���չһ������̼�����������ó�ʱ��������������Բ��ּ�ͥ���·ݵ�ƽ��ÿ���ó�ʱ�������һ�γ������飬�������� �������ݻ�������ͼ��ʾ��������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺

(1)���γ��������˶��ٸ���ͥ��
(2)��ͼ���е�Ƶ���ֲ�ֱ��ͼ����������
(3)���ó�ʱ���� 1 Сʱ��1.5 Сʱ�IJ��ֶ�Ӧ���� ��Բ�ĽǵĶ�����
(4)���������г���ͥ�� 1 600 ����������Ƹ������ó�ʱ�䲻���� 1.5 Сʱ��Լ�ж��ٸ���ͥ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��е� A��a��1��3����B��a+2��2a��1��
(1)���߶�AB��x�ᣬ���A��B�����ꣻ
(2)����B��x��ľ����ǵ�A��y��ľ���2��ʱ�����B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽���뷢�֣�
̽��һ������֪���������ε�һ����ǵ������������ڵ������ڽǵĺͣ���ô�������ε�һ���ڽ����������ڵ�������ǵĺ�֮����ں���������ϵ�أ�
��֪����ͼ1����FDC���ECD�ֱ�Ϊ��ADC��������ǣ���̽����A���FDC+��ECD��������ϵ��
̽�����������ε�һ���ڽ����������ڽǵ�ƽ�������еĶ۽�֮���к��ֹ�ϵ��
��֪����ͼ2���ڡ�ADC�У�DP��CP�ֱ�ƽ�֡�ADC�͡�ACD����̽����P���A��������ϵ��
̽������������ADC��Ϊ�����ı���ABCD�أ�
��֪����ͼ3�����ı���ABCD�У�DP��CP�ֱ�ƽ�֡�ADC�͡�BCD����������������̽����P���A+��B��������ϵ��
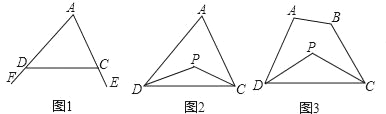
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ռ�����֪ʶ����ǿ������ʶ��ij��ѧijרҵѧԺ�ӱ�רҵ450���������ȡ��30��ѧ���μӻ���֪ʶ���ԣ��÷�![]() ʮ����
ʮ����![]() �����ͼ��ʾ��
�����ͼ��ʾ��
![]() ��30��ѧ���IJ��Գɼ�����������λ����ƽ�����ֱ��Ƕ��٣�
��30��ѧ���IJ��Գɼ�����������λ����ƽ�����ֱ��Ƕ��٣�
![]() ѧԺ���ó�2000Ԫ����Ʒ�������Գɼ������ѧ������Ʒ��Ϊ���ȣ��ɼ�Ϊ10�ֵ�Ϊһ�ȣ��ɼ�Ϊ8�ֺ�9�ֵ�Ϊ���ȣ��ɼ�Ϊ7�ֵ�Ϊ���ȣ�ѧԺҪ��һ�Ƚ����𣬶��Ƚ��������Ƚ�����ֱ�ռ
ѧԺ���ó�2000Ԫ����Ʒ�������Գɼ������ѧ������Ʒ��Ϊ���ȣ��ɼ�Ϊ10�ֵ�Ϊһ�ȣ��ɼ�Ϊ8�ֺ�9�ֵ�Ϊ���ȣ��ɼ�Ϊ7�ֵ�Ϊ���ȣ�ѧԺҪ��һ�Ƚ����𣬶��Ƚ��������Ƚ�����ֱ�ռ![]() ��
��![]() ��
��![]() ����ÿ�ֽ�Ʒ�ĵ��۸�Ϊ����Ԫ��
����ÿ�ֽ�Ʒ�ĵ��۸�Ϊ����Ԫ��
![]() �����רҵѧԺ��ѧ��ȫ���μӲ��ԣ���
�����רҵѧԺ��ѧ��ȫ���μӲ��ԣ���![]() �ʵĽ��������£�����Ԥ���רҵѧԺ�����ó����ٽ���������ѧ��������һ�Ƚ�����Ϊ����Ԫ��
�ʵĽ��������£�����Ԥ���רҵѧԺ�����ó����ٽ���������ѧ��������һ�Ƚ�����Ϊ����Ԫ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com