
【题目】在直角坐标平面内,![]() 为原点,点
为原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 轴. 点
轴. 点![]() 与点
与点![]() 关于原点对称,直线
关于原点对称,直线![]() (
(![]() 为常数)经过点
为常数)经过点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() .
.
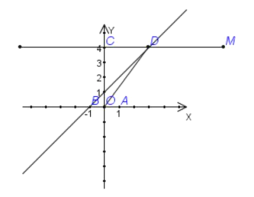
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)在![]() 轴上有一点
轴上有一点![]() ,使
,使![]() 的面积为
的面积为![]() ,求
,求![]() 点的坐标;
点的坐标;
(3)在![]() 轴的正半轴上是否存在一点
轴的正半轴上是否存在一点![]() ,使得
,使得![]() 为等腰三角形,若存在,求出点
为等腰三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
科目:初中数学 来源: 题型:
【题目】下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家______ 千米,张强从家到体育场用了______ 分钟;
(2)体育场离文具店______ 千米;
(3)张强在文具店逗留了______ 分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
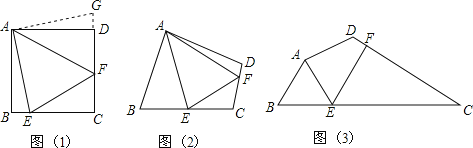
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
(发现证明)小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
(类比引申)如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
(探究应用)如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,∠EAF=75°且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点![]() 表示
表示![]() ,点
,点![]() 表示
表示![]() ,点
,点![]() 表示
表示![]() .动点
.动点![]() 从点
从点![]() 出发,沿数轴正方向以每秒
出发,沿数轴正方向以每秒![]() 个单位的速度匀速运动;同时,动点
个单位的速度匀速运动;同时,动点![]() 从点
从点![]() 出发,沿数轴负方向以每秒
出发,沿数轴负方向以每秒![]() 个单位的速度匀速运动.设运动时间为
个单位的速度匀速运动.设运动时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点相遇?相遇点
两点相遇?相遇点![]() 所对应的数是多少?
所对应的数是多少?
(2)在点![]() 出发后到达点
出发后到达点![]() 之前,求
之前,求![]() 为何值时,点
为何值时,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等;
的距离相等;
(3)在点![]() 向右运动的过程中,
向右运动的过程中,![]() 是
是![]() 的中点,在点
的中点,在点![]() 到达点
到达点![]() 之前,求
之前,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被 这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已 知菱形的边长为 4,且有一个内角为 60°,设它的等积线段长为 m,则 m 的取值范围是( )
A. m=4 或 m=4![]() B. 4≤m≤4
B. 4≤m≤4 ![]() C. 2
C. 2 ![]() D. 2
D. 2 ![]() ≤m≤4
≤m≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
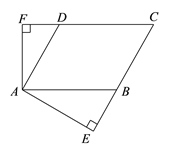
【题目】如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.
(1)求∠C的度数;
(2)已知DF的长是关于![]() 的方程
的方程![]() -
-![]() -6=0的一个根,求该方程的另一个根.
-6=0的一个根,求该方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,求他选中《九章算术》的概率;
(2)小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容,用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com