
【题目】如图1,在矩形ABCD中,点A(1,1),B(3,1),C(3,2),反比例函数y=![]() (x>0)的图象经过点D,且与AB相交于点E,
(x>0)的图象经过点D,且与AB相交于点E,

(1)求反比例函数的解析式;
(2)过点C、E作直线,求直线CE的解析式;
(3)如图2,将矩形ABCD沿直线CE平移,使得点C与点E重合,求线段BD扫过的面积.

【答案】(1)反比例函数的解析式为y=![]() ; (2)直线CE的解析式为y=x-1;(3) 3.
; (2)直线CE的解析式为y=x-1;(3) 3.
【解析】分析:(1)由矩形的性质求得点D的坐标,即可求得k;(2)根据反比例函数的解析式求点E的坐标,用待定系数法求直线CE的解析式;(3)BD扫过的面积是一个平行四边形,它的面积=2S△BB′D′.
详解:(1)由题意得AD=CB=1,故点D的坐标为(1,2),
∵函数y=![]() 的图象经过点D(1,2),
的图象经过点D(1,2),
∴2=![]() .∴m=2,
.∴m=2,
∴反比例函数的解析式为y=![]() ;
;
(2)当y=1时,1=![]() .∴x=2,∴E(2,1),
.∴x=2,∴E(2,1),
设直线CE的解析式为y=kx+b,根据题意得![]()
解得![]()
∴直线CE的解析式为y=x-1;
(3)∵矩形ABCD沿直线CE平移,使得点C与点E重合,点D(0,1),B'(2,0),
S四边形BDD′B′=2S△BB′D′=2×![]() ×3×1=3.
×3×1=3.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某市公交快速通道开通后,为响应市政府“绿色出行”的号召,家住新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A地在数轴上表示的数为-16,AB两地相距50个单位长度.小明从A地出发去B地,以每分钟2个单位长度的速度行进,第一次他向左1单位长度,第二次向右2单位长度,第三次再向左3单位长度,第四次又向右4单位长度…,按此规律行进.
![]()
(1)求出B地在数轴上表示的数;
(2)若B地在原点的右侧,经过第8次行进后小明到达点P,此时点P与点B相距几个单位长度?8次运动完成后一共经过了几分钟?
(3)若经过n次(n为正整数)行进后,小明到达点Q,请你直接写出:点Q在数轴上表示的数应如何表示?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,已知AB=6,BC=9, ![]() .对角线AC、BD交于点O.动点P在边AB上,⊙P经过点B,交线段PA于点E.设BP= x.
.对角线AC、BD交于点O.动点P在边AB上,⊙P经过点B,交线段PA于点E.设BP= x.
(1)求AC的长;
(2)设⊙O的半径为y,当⊙P与⊙O外切时,求y关于x的函数解析式,并写出定义域;
(3)如果AC是⊙O的直径,⊙O经过点E,求⊙O与⊙P的圆心距OP的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.
(1)点C的坐标为 (用字母n表示)
(2)如果△ABC的面积为5.5,求n的值;
(3)在(2)的条件下,坐标平面内是否存在一点M,使以点M、A、B为顶点组成的三角形与△ABC全等?如果存在画出符合要求的图形,求出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
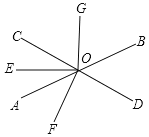
【题目】如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOC,∠AOF的度数;
(2)求∠EOF与∠BOG是否相等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取甲乙两所学校的20名学生的数学成绩进行分析:
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据:按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
|
|
|
|
|
|
|
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | m | 115.25 |
经统计,表格中m的值是 .
得出结论:
a若甲学校有400名初二学生,估计这次考试成绩80分以上人数为 .
b可以推断出 学校学生的数学水平较高,理由为 .(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com