
 和直线y=kx+2(k是常数)相交于点A(x1,y1)和点B(x2,y2),(x1<x2)且
和直线y=kx+2(k是常数)相交于点A(x1,y1)和点B(x2,y2),(x1<x2)且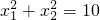 .
.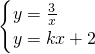 ,
, =kx+2,即kx2+2x-3=0,
=kx+2,即kx2+2x-3=0, ,
, ,x1x2=-
,x1x2=-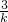 ,
,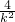 +
+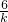 =10,
=10, (不合题意,舍去)或k=1,
(不合题意,舍去)或k=1, 联立,
联立,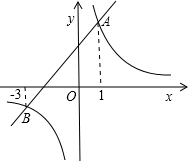


科目:初中数学 来源:2012年初中毕业升学考试(四川广安卷)数学(带解析) 题型:解答题
如图,已知双曲线 和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=
和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=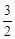 .
.
(1)求双曲线和和直线的解析式.
(2)求△AOB的面积.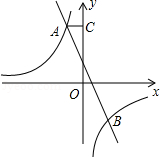
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《反比例函数》(03)(解析版) 题型:解答题
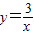 和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.
和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.查看答案和解析>>
科目:初中数学 来源:2004年湖北省荆门市中考数学试卷(解析版) 题型:解答题
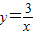 和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.
和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.查看答案和解析>>
科目:初中数学 来源:2011-2012学年江西省南昌市九年级下学期第二次联考数学试卷(解析版) 题型:解答题
已知双曲线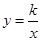 和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.
和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.
1.求双曲线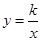 的解析式;
的解析式;
2.当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线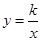 另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com