
【题目】如图,一艘船以每小时![]() 海里的速度向西南方向航行,在
海里的速度向西南方向航行,在![]() 处观测灯塔
处观测灯塔![]() 在船的南偏西
在船的南偏西![]() 的方向,航行
的方向,航行![]() 分钟后到达
分钟后到达![]() 处,这时灯塔
处,这时灯塔![]() 恰好在船的正西方向.已知距离此灯塔
恰好在船的正西方向.已知距离此灯塔![]() 海里以内的海区有暗礁,这艘船继续沿西南方向航行是否有触礁的危险?为什么?(参考数据:
海里以内的海区有暗礁,这艘船继续沿西南方向航行是否有触礁的危险?为什么?(参考数据:![]() ,
,![]() )
)

【答案】这艘船继续沿西南方向航行有触礁的危险,理由详见解析.
【解析】
首先过点M作MC⊥AB于C,根据题意可得:∠WAC=∠SAC=45°,∠SAM=75°,即可求得∠1与∠2的度数,然后设MC=x(海里),由三角函数的知识,即可求得AC=![]() x,AB=6,又由AC=AB+BC,即可得方程:
x,AB=6,又由AC=AB+BC,即可得方程:![]() x=6+x,解此方程即可求得答案.
x=6+x,解此方程即可求得答案.
这艘船继续沿西南方向航行有触礁的危险.理由如下:
过点M作MC⊥AB于C.
由题意得:∠WAC=∠SAC=45°,∠SAM=75°,∴∠1=∠SAM﹣∠SAC=30°.
设MC=x(海里).在Rt△MAC中,AC=![]() x(海里).
x(海里).
∵灯塔M恰好在船的正西方向,∴MB∥WA,∴∠2=∠WAC=45°.
在Rt△MAC中,设BC=MC=x(海里),∴AB=40×![]() =6(海里).
=6(海里).
∵AC=AB+BC,∴![]() x=6+x,解得:x=3
x=6+x,解得:x=3![]() +3.
+3.
∵MC=3![]() +3≈8.19海里<9海里,∴有触礁的危险.
+3≈8.19海里<9海里,∴有触礁的危险.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
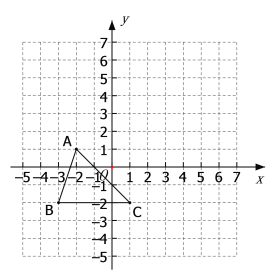
【题目】已知:如图,把![]() 向上平移
向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度,得到
个单位长度,得到![]() ;
;
(1)写出![]() 的坐标;
的坐标;
(2)求出![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,且
轴上,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大长方形是由四个小长方形拼成的,请根据此图填空:x2+(p+q)x+pq=x2+px+qx+pq=( )( ).
说理验证
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq=x2+px+qx+pq=(x2+px)+()= =( )( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用
例题 把x2+3x+2分解因式.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式分解因式:
(1)x2﹣7x+12; (2)(y2+y)2+7(y2+y)﹣18.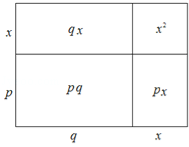
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有![]() 、
、![]() 、
、![]() 三艘船正在捕鱼作业,
三艘船正在捕鱼作业,![]() 船突然出现故障,向
船突然出现故障,向![]() 、
、![]() 两船发出紧急求救信号,此时
两船发出紧急求救信号,此时![]() 船位于
船位于![]() 船的北偏西
船的北偏西![]() 方向,距
方向,距![]() 船
船![]() 海里的海域,
海里的海域,![]() 船位于
船位于![]() 船的北偏东
船的北偏东![]() 方向,同时又位于
方向,同时又位于![]() 船的北偏东
船的北偏东![]() 方向.
方向.

(1)求![]() 的度数;
的度数;
![]() 船以每小时
船以每小时![]() 海里的速度前去救援,问多长时间能到出事地点.(结果精确到
海里的速度前去救援,问多长时间能到出事地点.(结果精确到![]() 小时).(参考数据:
小时).(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步营造扫黑除恶专项斗争的浓厚宣传氛围,推进平安校园建设,甲、乙两所学校各租用一辆大巴车组织部分师生,分别从距目的地240千米和270千米的两地同时出发,前往“研学教育”基地开展扫黑除恶教育活动,已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍,甲校师生比乙校师生晚1小时到达目的地,分别求甲、乙两所学校师生所乘大巴车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有位农场主有一大片田地,其形状恰好是一个平行四边形,并且在对角线![]() 上有一口水井
上有一口水井![]() .农场主临死前留下遗嘱,把两块三角形的田地(即图中阴影部分)给小儿子,剩下的全部给大儿子,至于水井
.农场主临死前留下遗嘱,把两块三角形的田地(即图中阴影部分)给小儿子,剩下的全部给大儿子,至于水井![]() ,正好两儿子共用,由于平行四边形两边长不同,所以遗嘱公布之后,亲友们七嘴八舌,议论纷纷,认为这个分配不公平,那么你认为________.(填“公平”或“不公平”)理由是________.
,正好两儿子共用,由于平行四边形两边长不同,所以遗嘱公布之后,亲友们七嘴八舌,议论纷纷,认为这个分配不公平,那么你认为________.(填“公平”或“不公平”)理由是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com