
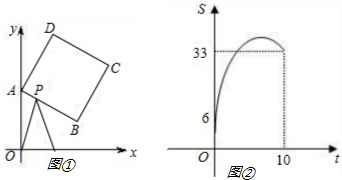
 解:(1)10,(14,14);
解:(1)10,(14,14); t,
t, (1+t)(12-
(1+t)(12- t)=-
t)=-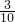 t2+
t2+ t+6,
t+6,
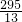 .
. t,因此OM=12-
t,因此OM=12- t,根据三角形的面积公式即可求出S,t的函数关系式.根据函数的性质即可求出S的最大值及对应的t的值;
t,根据三角形的面积公式即可求出S,t的函数关系式.根据函数的性质即可求出S的最大值及对应的t的值; ①P在AB上,②P在BC上,③P在BC上,④P在AD上.
①P在AB上,②P在BC上,③P在BC上,④P在AD上. ,如果OP=OQ,那么PM=
,如果OP=OQ,那么PM= OQ,即
OQ,即 t=
t= ,解得t=1.
,解得t=1. CP=
CP= (t-20),因此PM=RN=14-
(t-20),因此PM=RN=14- (t-20)=30-
(t-20)=30- t,根据①的解题思路可知:PM=
t,根据①的解题思路可知:PM= OQ,即30-
OQ,即30- t=
t= ,解得t=
,解得t=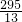 .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
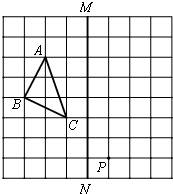 21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)查看答案和解析>>
科目:初中数学 来源: 题型:
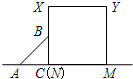 (2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
(2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com