
【题目】如图1,图2,分别是吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A点距地面的高度是多少米?(精确到0.1米)(参考数据:sin10°=cos80°=0.17,cos10°=sin80°=0.98,sin20°=cos70°=0.34,tan70°=2.75,sin70°=0.94)
【答案】【解答】解:由题可知:如图,BH⊥HE,AE⊥HE,CD=2,BC=4
∠BCH=30°,∠ABC=80°,∠ACE=70°
∵∠BCH+∠ACB+∠ACE=180°
∴∠ACB=80°
∵∠ABC=80°
∴∠ABC=∠ACB
∴AB=AC
过点A作AM⊥BC于M,
∴CM=BM=2
∵在Rt△ACM中,CM=2,∠ACB=80°
∴![]() =cos∠ACB=cos80°≈0.17
=cos∠ACB=cos80°≈0.17
∴AC=![]()
∵在Rt△ACE中,AC=![]() ,∠ACE=70°
,∠ACE=70°
∴![]() =sin∠ACE=sin70°≈0.94
=sin∠ACE=sin70°≈0.94
∴AE=![]() ×0.94=
×0.94=![]() ≈11.1
≈11.1
故可得点A到地面的距离为13.1米.
【解析】先求得AC=BC然后利用解直接三角形的方法求出AC,再在Rt△AEC中解出AE的长,从而求出A到地面的高度为AE+2.


科目:初中数学 来源: 题型:
【题目】一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
(1)求抛物线的解析式;
(2)问:当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.
(4)设抛物线顶点为M,连接BP,BM,MQ,问:是否存在t的值,使以B,Q,M为顶点的三角形与以O,B,P为顶点的三角形相似?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A1B1A2 , △A2B2A3 , △A3B3A4 , …,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA1=1,则OA2015的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.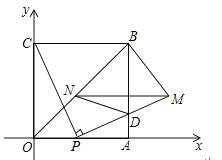
(1)求点M的坐标(用含t的代数式表示);
(2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.
(3)当t为何值时,四边形BNDM的面积最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
A.圆形铁片的半径是4cm
B.四边形AOBC为正方形
C.弧AB的长度为4πcm
D.扇形OAB的面积是4πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线y=ax2+bx+n(a≠0)过E,A′两点.
(1)填空:∠AOB= °,用m表示点A′的坐标:A′( , );
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且![]() =
=![]() 时,△D′OE与△ABC是否相似?说明理由;
时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com