
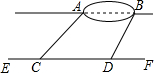
 某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.
某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.  快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
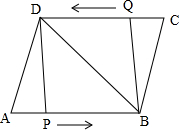 如图,已知?ABCD中,AD=8cm,AB=10cm,BD=12cm,点P从点A出发,以1cm/s的速度向点B运动,同时点Q从点C出发以相同的速度向点D运动,设运动时间为t.
如图,已知?ABCD中,AD=8cm,AB=10cm,BD=12cm,点P从点A出发,以1cm/s的速度向点B运动,同时点Q从点C出发以相同的速度向点D运动,设运动时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
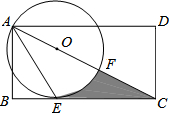 如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O为圆心作圆,使⊙O经过A,E两点,⊙O交AC于点F,
如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O为圆心作圆,使⊙O经过A,E两点,⊙O交AC于点F,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com