
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

【答案】(1) A(﹣1,0),B(3,0);(2)存在,P(![]() );(3) m=﹣1或﹣
);(3) m=﹣1或﹣![]() .
.
【解析】试题分析:(1)将![]() 化为交点式,即可得到
化为交点式,即可得到![]() 两点的坐标;
两点的坐标;
(2)先用待定系数法得到抛物线C1的解析式,过点P作PQ∥y轴,交BC于Q,用待定系数法得到直线BC的解析式,再根据三角形的面积公式和配方法得到![]() 面积的最大值;
面积的最大值;
(3)先表示出![]() 再分两种情况:①
再分两种情况:①![]() 时;
时;
②![]() 时,讨论即可求得
时,讨论即可求得![]() 的值.
的值.
试题解析:(1)![]()
∵m≠0,
∴当y=0时,![]()
∴A(1,0),B(3,0);
(2)设![]() ,将A. B.C三点的坐标代入得:
,将A. B.C三点的坐标代入得:
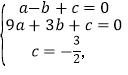 解得
解得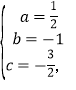
故![]()
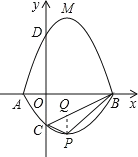
如图:过点P作PQ∥y轴,交BC于Q,
由B.C的坐标可得直线BC的解析式为:![]()
设![]() 则
则![]()
![]()
![]()
当![]() 时,
时,![]() 有最大值,
有最大值,![]()
![]()
![]()
(3)![]()
顶点M坐标(1,4m),
当x=0时,y=3m,
∴D(0,3m),B(3,0),
![]()
![]()
![]()
当△BDM为Rt△时有:![]() 或
或![]()
![]() 时有:
时有:![]()
解得m=1(∵m<0,∴m=1舍去);
![]() 时有:
时有:![]()
解得![]() (
(![]() 舍去).
舍去).
综上,m=1或![]() 时,
时,![]() 为直角三角形.
为直角三角形.


科目:初中数学 来源: 题型:
【题目】学校组织中国共产党第十九次全国代表大会知识问答,共设有20道选择题,各题分值相同,每题必答.下表记录了A、B、D三名参赛学生的得分情况:
参赛学生 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
D | 14 | 6 | 64 |
则参赛学生E的得 分可能 是( )
A.93B.87C.66D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距240千米的A,B两地同时相向匀速出发,甲车出发0.5小时后发现有东西落在出发地A地,于是立即按原速沿原路返回,在A地取到东西后立即以原速继续向B地行驶,并在途中与乙车第一次相遇,相遇后甲、乙两车继续以各自的速度朝着各自的方向匀速行驶,当乙车到达A地后,立即掉头以原速开往B地(甲车取东西、掉头和乙车掉头的时间均忽略不计).两车之间的距离y(千米)与甲车出发的时间x(小时)之间的部分关系如图所示,则当乙车到达B地时,甲车与B地的距离为_____千米.
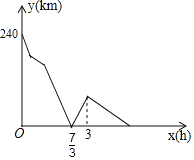
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=2,BC=1.5,矩形在直线上绕其右下角的顶点B向右第一次旋转90°至图①位置,再绕右下角的顶点继续向右第二次旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当![]() 时,画出最多直线的条数分别是:
时,画出最多直线的条数分别是:
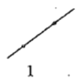
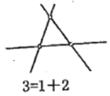
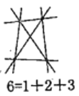
过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出![]() 条直线.
条直线.
请你比照上述方法,解决下列问题:(要求作图分析)
(1)平面上的20条直线最多有多少个交点?
(2)平面上的100条直线最多可以把平面分成多少个部分?平面上![]() 条直线最多可以把平面分成多少个部分?
条直线最多可以把平面分成多少个部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段引导市民节约用水。某市规定如下用水收费标准:每月每户的用水不超过6![]() 时,水费按正常收费;超过6
时,水费按正常收费;超过6![]() 时,超过的部分收较高水费。该市某户居民今年2月份的用水量为9
时,超过的部分收较高水费。该市某户居民今年2月份的用水量为9![]() ,缴纳水费为27元;3月份的用水量为11
,缴纳水费为27元;3月份的用水量为11![]() ,缴纳水费为37元。
,缴纳水费为37元。
(1)求在限定量以内每吨多少元?超出部分的水费每吨多少元?
(2)若该市某居民今年4月份的用水量为13![]() . 则应缴纳水费多少元?
. 则应缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成一项工作,如果安排两个人合做,要![]() 天才能完成.开始先安排一些人做
天才能完成.开始先安排一些人做![]() 天后,又增加
天后,又增加![]() 人和他们一起做
人和他们一起做![]() 天,结果完成了这项工作的一半,假设这些人的工作效率相同.
天,结果完成了这项工作的一半,假设这些人的工作效率相同.
(1)开始安排了多少名工人?
(2)如果要求再用![]() 天做完剩余的全部工作,还需要再增加几人一起做?
天做完剩余的全部工作,还需要再增加几人一起做?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com