

���� ��1������A��AD��BC������ΪD����������������Ǻ���ֵ�����BD=$\frac{1}{2}$��AD=$\frac{\sqrt{3}}{2}$��������������ε������ʽ���㼴�ɣ�
��2������������õ�������ABC�����=$\frac{1}{2}$����AB+BC+AC��r��Ȼ������r��ֵ��
��3����֤����ADF�ա�BED�ա�CFE���Ӷ��õ���ADF���ܳ�=a+b���ɣ�1����֪��������ADF�����$\frac{1}{3}��$$\frac{\sqrt{3}}{8}��{a}^{2}-{b}^{2}��$��Ȼ�����ã�2���Ľ�����⼴�ɣ�
��� �⣺��1����ͼ1��ʾ������A��AD��BC������ΪD��
��AD��BC��
���ADB=90�㣮
�ߡ�ABC�ǵȱ������Σ�
���B=60�㣮
��BD=$\frac{1}{2}$AB=$\frac{1}{2}$��AD=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$��
��S��ABC=$\frac{1}{2}��1��\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$��
�ʴ�Ϊ��$\frac{\sqrt{3}}{4}$��
��2����ͼ2��ʾ������Բ��O���е�D��
��BC��ԲO�����ߣ�
��DO��BC��
���BCO�����=$\frac{1}{2}CB•r$��
ͬ������BAO�����=$\frac{1}{2}$AB•r����ACO�����=$\frac{1}{2}AC•r$��
��������ABC�����=$\frac{1}{2}$����AB+BC+AC��r��
��r=$\frac{4}{\frac{1}{2}��8}$=1��
��3���ߡ�ABC���DEF�ǵȱ������Σ�
���B=��A=60��DE=EF����DEF=60�㣮
�ߡ�B+��BDE=��EDF+FEC��
���BDE=��FEC��
�ڡ�BED�͡�CFE�У�$\left\{\begin{array}{l}{��B=��C}\\{��BDE=��FEC}\\{DE=EF}\end{array}\right.$��
���BED�ա�CFE��
��ͬ������BED�ա�CFE�ա�ADF��
��AD=FC��
��AD+AF=AF+FC=a��
��AD+AF+DF=a+b��
�ɣ�1����֪S��ACB=$\frac{\sqrt{3}}{4}{a}^{2}$��S��DEF=$\frac{\sqrt{3}}{4}$b2��
��S��ADF=$\frac{1}{3}$��$\frac{\sqrt{3}}{4}$����a2-b2����
�ɣ�2����֪��r=$\frac{\frac{1}{3}��\frac{\sqrt{3}}{4}����{a}^{2}-{b}^{2}��}{\frac{1}{2}����a+b��}$=$\frac{\sqrt{3}}{6}$��a-b����
���� ������Ҫ������������ε�����Բ���ȱ������ε����ʡ�ȫ�������ε����ʺ��ж������ߵ����ʣ����������ADF���ܳ�������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij��Ϊ�ӹ̳�90�ף���30�ף��Ӷ���Ϊ6�ף�ӭˮ�ºͱ�ˮ�¶���1��1�ĺ���������εķ����ӣ�Ҫ����ӼӸ�2�ף���ˮ���¶ȸ�Ϊ1��1.5����֪�Ӷ������䣬���Ӻ��������Ӷ���ƽ���ף�
ij��Ϊ�ӹ̳�90�ף���30�ף��Ӷ���Ϊ6�ף�ӭˮ�ºͱ�ˮ�¶���1��1�ĺ���������εķ����ӣ�Ҫ����ӼӸ�2�ף���ˮ���¶ȸ�Ϊ1��1.5����֪�Ӷ������䣬���Ӻ��������Ӷ���ƽ���ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���A����Ϊ��2��3���������������Ƿ���ڵ�B��ʹ�á�OABΪֱ�������Σ�
��ͼ����ƽ��ֱ������ϵ�У���A����Ϊ��2��3���������������Ƿ���ڵ�B��ʹ�á�OABΪֱ�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����x��ǧ�ˣ� | 1 | 2 | 3 | 4 | 5 |
| �ۼ�y��Ԫ�� | 2.1 | 4.2 | 6.3 | 8.4 | 10.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
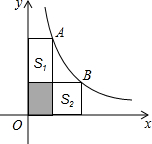 ��ͼ����A��B��˫����y=$\frac{3}{x}$�ϵĵ㣬�ֱ��A��B������x�ᡢy�������߶Σ���S��Ӱ=1����S1+S2=4��
��ͼ����A��B��˫����y=$\frac{3}{x}$�ϵĵ㣬�ֱ��A��B������x�ᡢy�������߶Σ���S��Ӱ=1����S1+S2=4���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com