
分析 设t=$\sqrt{\frac{8a-1}{3}}$,则a=$\frac{3{t}^{2}+1}{8}$,分别化简a+$\frac{a+1}{3}$$\sqrt{\frac{8a-1}{3}}$得$\frac{1}{8}$(t+1)3,a-$\frac{a+1}{3}$$\sqrt{\frac{8a-1}{3}}$=-$\frac{1}{8}$(t+1)3,继而可得原式=$\frac{1}{2}$(t+1)-$\frac{1}{2}$(t-1)=1.
解答 解:设t=$\sqrt{\frac{8a-1}{3}}$,则a=$\frac{3{t}^{2}+1}{8}$,
∴a+$\frac{a+1}{3}$$\sqrt{\frac{8a-1}{3}}$=$\frac{3{t}^{2}+1}{8}$+$\frac{\frac{3{t}^{2}+1}{8}+1}{3}$•t
=$\frac{3{t}^{2}+1}{8}$+$\frac{1}{3}$•$\frac{3{t}^{2}+9}{8}$•t
=$\frac{3{t}^{2}+1}{8}$+$\frac{{t}^{2}+3}{8}$•t
=$\frac{3{t}^{2}+1+{t}^{3}+3t}{8}$
=$\frac{1}{8}$(t+1)3,
a-$\frac{a+1}{3}$$\sqrt{\frac{8a-1}{3}}$=$\frac{3{t}^{2}+1}{8}$-$\frac{\frac{3{t}^{2}+1}{8}+1}{3}$•t
=$\frac{3{t}^{2}+1}{8}$-$\frac{1}{3}$•$\frac{3{t}^{2}+9}{8}$•t
=$\frac{3{t}^{2}+1}{8}$-$\frac{{t}^{2}+3}{8}$•t
=$\frac{{t}^{3}+3t-3{t}^{2}-1}{8}$
=-$\frac{1}{8}$(t+1)3,
∴原式=$\frac{1}{2}$(t+1)-$\frac{1}{2}$(t-1)
=$\frac{1}{2}$(t+1-t+1)
=$\frac{1}{2}$×2
=1,
故答案为:1.
点评 本题主要考查整式的化简求值,利用换元的方法化简两个立方根内被开方数是解题的关键.


科目:初中数学 来源: 题型:填空题
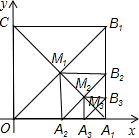 如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以A1M1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以A1M2为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;…依此类推,这样作的第n个正方形对角线交点Mn的坐标是($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$).
如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以A1M1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以A1M2为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;…依此类推,这样作的第n个正方形对角线交点Mn的坐标是($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角三角形纸板ABP的直角顶点P在直线l上,AP=3,BP=4,分别作AC⊥l于点C,BD⊥l于点D,若将三角形纸板在平面内绕点P旋转(点C、D、P互不重合),请直接写出旋转过程中线段CD、AC、BD的数量关系.
如图,直角三角形纸板ABP的直角顶点P在直线l上,AP=3,BP=4,分别作AC⊥l于点C,BD⊥l于点D,若将三角形纸板在平面内绕点P旋转(点C、D、P互不重合),请直接写出旋转过程中线段CD、AC、BD的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$或$-\frac{5}{4}$ | B. | $\frac{3}{4}$或$\frac{5}{4}$ | C. | $\frac{3}{4}$ | D. | -$\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
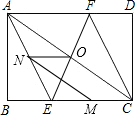 矩形ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F,连接EF,点M为EC的中点,N点为AE上的一个动点,AB=6
矩形ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F,连接EF,点M为EC的中点,N点为AE上的一个动点,AB=6查看答案和解析>>
科目:初中数学 来源: 题型:解答题
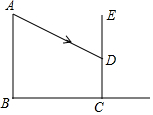 如图,一位同学想利用建筑物的影子测量建筑物AB的高度,他在某一时刻测得直立的标杆高为1m时,影长为1.2m,他立即又测量建筑物的影子,因建筑物AB靠近另一个建筑物CE,所以AB的影子没有完全落在地上,一部分影子落在墙上,他测得地上部分的影子长BC为7.2m,又测得墙上部分的影子高CD为1.2m,请你帮他计算建筑物AB的高度.
如图,一位同学想利用建筑物的影子测量建筑物AB的高度,他在某一时刻测得直立的标杆高为1m时,影长为1.2m,他立即又测量建筑物的影子,因建筑物AB靠近另一个建筑物CE,所以AB的影子没有完全落在地上,一部分影子落在墙上,他测得地上部分的影子长BC为7.2m,又测得墙上部分的影子高CD为1.2m,请你帮他计算建筑物AB的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com