
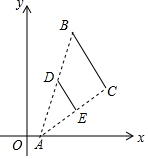
 如图,线段BC的两端点的坐标分别为B(3,7),C(6,3),以点A(1,0)为位似中心,将线段BC缩小为原来的$\frac{1}{2}$后得到线段DE,则端点D的坐标为( )
如图,线段BC的两端点的坐标分别为B(3,7),C(6,3),以点A(1,0)为位似中心,将线段BC缩小为原来的$\frac{1}{2}$后得到线段DE,则端点D的坐标为( )| A. | (1,$\frac{7}{2}$) | B. | (2,$\frac{7}{2}$) | C. | (1,2) | D. | (2,2) |
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 求不等式组$\left\{\begin{array}{l}{3x+3>5(x-1)①}\\{\frac{2x-2}{3}-1≤\frac{3x}{2}②}\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.
求不等式组$\left\{\begin{array}{l}{3x+3>5(x-1)①}\\{\frac{2x-2}{3}-1≤\frac{3x}{2}②}\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,抛物线y=x2-4x与x轴正半轴交于点A,其顶点为M,将这条抛物线绕点O旋转180°后得到的抛物线与x轴负半轴交于点B,其顶点记为N,连结AM、MB、BN、NA,则四边形AMBN的面积为32.
如图,在平面直角坐标系中,抛物线y=x2-4x与x轴正半轴交于点A,其顶点为M,将这条抛物线绕点O旋转180°后得到的抛物线与x轴负半轴交于点B,其顶点记为N,连结AM、MB、BN、NA,则四边形AMBN的面积为32.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
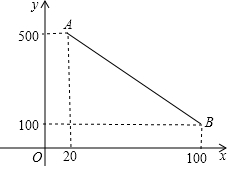 小明家买了一台充电式自动扫地机,每次完成充电后,在使用时扫地机会自动根据设定扫地时间,来确定扫地的速度(以使每次扫地结束时尽量把所储存的电量用完),如图是“设定扫地时间”与“扫地速度”之间的函数图象(线段AB),其中设定扫地时间为x分钟,扫地速度为y平方分米/分钟.
小明家买了一台充电式自动扫地机,每次完成充电后,在使用时扫地机会自动根据设定扫地时间,来确定扫地的速度(以使每次扫地结束时尽量把所储存的电量用完),如图是“设定扫地时间”与“扫地速度”之间的函数图象(线段AB),其中设定扫地时间为x分钟,扫地速度为y平方分米/分钟.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com