
 С�ŴӼ��ſ��ﳵȥ��λ�ϰ࣬����ƽ·�����A����������·�����B�����������·���﹤����λ�����õ�ʱ����·�̵Ĺ�ϵ��ͼ��ʾ���°���������ԭ·���أ�����ƽ·������·������·���ٶȷֱ𱣳ֺ�ȥ�ϰ�ʱһ�£�������˵������ȷ�ĸ����ǣ�������
С�ŴӼ��ſ��ﳵȥ��λ�ϰ࣬����ƽ·�����A����������·�����B�����������·���﹤����λ�����õ�ʱ����·�̵Ĺ�ϵ��ͼ��ʾ���°���������ԭ·���أ�����ƽ·������·������·���ٶȷֱ𱣳ֺ�ȥ�ϰ�ʱһ�£�������˵������ȷ�ĸ����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
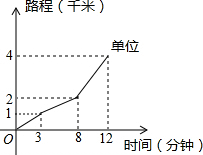
���� ��ͼ��ᡢ�����겻�ѿ����١��ڶ���ȷ��������·��·�̺�ʱ������ٶȼ����жϢ۴����°������·2ǧ����ʱ10���ӣ�����·1ǧ����ʱ2Сʱ��ƽ·1ǧ����ʱ3Сʱ���ʢ���ȷ��
��� �⣺��ͼ����Կ�����С����ʱ12���ӵ������4ǧ�ĵ�λ���ʢ١��ڶ���ȷ��
��ͼ����Կ���С���ϰ�ʱ������·��1ǧ�ף���ʱ8-3=5Сʱ���������µ��ٶ�Ϊ��1��5=0.2ǧ��/ʱ���ʢ۴���
С���°��ʱ������·2ǧ�ף���ʱ10Сʱ������·1ǧ�ף���ʱ2Сʱ��ƽ·1ǧ�ף���ʱ3Сʱ����15Сʱ���ʢ���ȷ�������3����ȷ��˵����
��ѡ��C��
���� ���⿼�����ú�����ͼ����ʵ�����⣬��ȷ���⺯��ͼ����������ʾ�����壬��������Ĺ��̣����ܹ�ͨ��ͼ��õ������������Ӧ�����


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
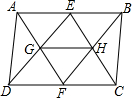 ��ͼ����?ABCD�У�E��F�ֱ�ΪAB��CD���е㣬��֤��GH=$\frac{1}{2}$DC��
��ͼ����?ABCD�У�E��F�ֱ�ΪAB��CD���е㣬��֤��GH=$\frac{1}{2}$DC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
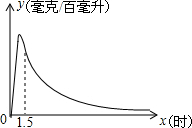 ʵ��������ʾ��һ����˺Ȱ��ͶȰƺ���ѪҺ�оƾ�����y������/�ٺ�������ʱ��x��Сʱ���Ĺ�ϵΪ����0��x��1.5ʱ��y��x�ɶ��κ�����ϵ����y=-200x2+400x����x��1.5ʱ��y��x�ɷ�����������ϵ����y=$\frac{k}{x}$��
ʵ��������ʾ��һ����˺Ȱ��ͶȰƺ���ѪҺ�оƾ�����y������/�ٺ�������ʱ��x��Сʱ���Ĺ�ϵΪ����0��x��1.5ʱ��y��x�ɶ��κ�����ϵ����y=-200x2+400x����x��1.5ʱ��y��x�ɷ�����������ϵ����y=$\frac{k}{x}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
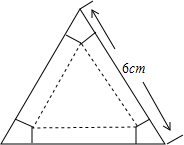 ��ͼ����һ��߳�Ϊ6cm����������ֽ�壬�����������Ǵ��ֱ��ȥһ���˴�ȫ�ȵ����Σ�����ͼ�е�������������һ���ǵ�ֱ������ֽ�У����ֽ�в���������ֵ�ǣ�������
��ͼ����һ��߳�Ϊ6cm����������ֽ�壬�����������Ǵ��ֱ��ȥһ���˴�ȫ�ȵ����Σ�����ͼ�е�������������һ���ǵ�ֱ������ֽ�У����ֽ�в���������ֵ�ǣ�������| A�� | $\sqrt{3}$cm2 | B�� | $\frac{3}{2}$$\sqrt{3}$cm2 | C�� | $\frac{9}{2}$$\sqrt{3}$cm2 | D�� | $\frac{27}{2}$$\sqrt{3}$cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
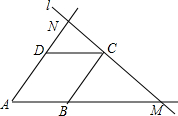 ��ͼ������ABCD�ı߳�Ϊ1��ֱ��l����C����AB���ӳ�����M����AD���ӳ�����N����$\frac{1}{AM}$+$\frac{1}{AN}$=1��
��ͼ������ABCD�ı߳�Ϊ1��ֱ��l����C����AB���ӳ�����M����AD���ӳ�����N����$\frac{1}{AM}$+$\frac{1}{AN}$=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
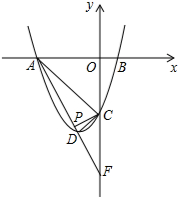 ��ͼ����֪������y=ax2+bx+c��x�ύ�ڵ�A��B����ֱ��AC��y=-x-6��y���ڵ�C����D�������ߵĶ��㣬�Һ�����Ϊ-2��
��ͼ����֪������y=ax2+bx+c��x�ύ�ڵ�A��B����ֱ��AC��y=-x-6��y���ڵ�C����D�������ߵĶ��㣬�Һ�����Ϊ-2���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com