练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
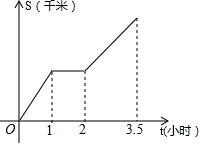
    4．星期天，小明从家出发，以15千米/小时的速度骑车去郊游，到达目的地休息一段时间后原路返回，已知小明行驶的路程s（千米）与时间t（小时）之间的函数关系如图所示，则小明返程的速度为（　　）
    A．15千米/小时B．10千米/小时C．6千米/小时D．无法确定

    分析 由往返路程相同结合速度=路程÷时间，即可求出小明返程的速度，此题得解．

    解答 解：15×1÷（3.5-2）=10（千米/小时），
    ∴小明返程的速度为10千米/小时．
    故选B．

    点评 本题考查了函数的图象，利用速度=路程÷时间求出小明返程的速度是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．先阅读材料再回答问题：如图线段AB=4，AC=1，BD=2，且AC⊥AB，BD⊥AB，点P在线段AB上运动，当AP=a时，则BP=4-a，PC=$\sqrt{1{+a}^{2}}$，PD=$\sqrt{4{+（4-a）}^{2}}$，由此可求得CP+DP的最小值为5．那么请问：代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+（5-x）}^{2}}$的最小值为（　　）
    A．10B．2$\sqrt{10}$C．$\sqrt{61}$D．$\sqrt{41}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

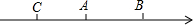    15．如图，数轴上A、B两点表示的数分别为-1和$\sqrt{3}$，点A是BC的中点，则点C所表示的数（　　）
    A．-2-$\sqrt{3}$B．-1-$\sqrt{3}$C．-2+$\sqrt{3}$D．1+$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．一个正多边形的一个内角是与其相邻的一个外角的3倍，则这个正多边形的边数是8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P=90°，PM交AB于点E，PN交CD于点F．

    （1）当△PMN所放位置如图①所示时，求出∠PFD与∠AEM的数量关系；
    （2）当△PMN所放位置如图②所示时，求证：∠PFD-∠AEM=90°；
    （3）在（2）的条件下，若MN与CD交于点O，且∠DON=15°，∠PEB=30°，求∠N的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

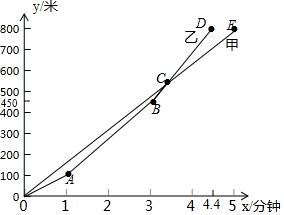    9．百舸竞渡，激情飞扬．为纪念爱国诗人屈原，某市举行龙舟赛．甲、乙两支龙舟队在比赛时，路程y（米）与时间x（分钟）之间的函数图象如图所示，根据图象回答下列问题：
    （1）最先达到终点的是乙队，比另一对早0.6分钟到达；
    （2）在比赛过程中，乙队在第1分钟和第3分钟时两次加速；
    （3）求在什么时间范围内，甲队领先？
    （4）相遇前，甲乙两队之间的距离不超过30m的时间范围是0＜x≤0.5或3≤x≤$\frac{10}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．若$\frac{a+b}{b}$=$\frac{8}{3}$，则$\frac{a}{b}$=$\frac{5}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．关于x的一元二次方程（a-1）x2-2x+1=0有两个不相等的实数根，则a的范围是a＜2且a≠1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

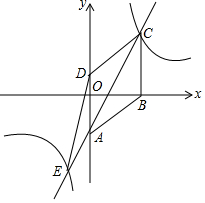    14．已知四边形ABCD是菱形，在平面直角坐标系中的位置如图，边AD经过原点O，已知A（0，-3），B（4，0），反比例函数图象经过点C，直线AC交双曲线另一支于点E，连接DE，CD，设反比例函数解析式为y1=$\frac{k}{x}$，直线AC解析式为y2=ax+b．
    （1）求反比例函数解析式；
    （2）当y1＜y2时，求x的取值范围；
    （3）求△CDE的面积．

    查看答案和解析>>

    同步练习册答案