
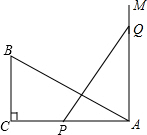
 如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由.
如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由. 分析 本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=5cm,可据此求出P点的位置.
②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
解答 解:根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,
$\left\{\begin{array}{l}{AP=BC}\\{PQ=AB}\end{array}\right.$,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=5cm;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中,
$\left\{\begin{array}{l}{AP=AC}\\{PQ=AB}\end{array}\right.$,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=10cm,
∴当点P与点C重合时,△ABC才能和△APQ全等.
综上所述,当点P位于AC的中点处或当点P与点C重合时,△ABC才能和△APQ全等.
点评 本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
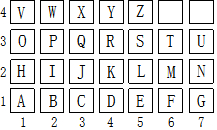 某个英文单词的字母顺序对应如上图中的有序数对分别为(6,2),(1,1),(6,3),(1,2),(5,3),请你把这个英文单词写出来为MATHS.
某个英文单词的字母顺序对应如上图中的有序数对分别为(6,2),(1,1),(6,3),(1,2),(5,3),请你把这个英文单词写出来为MATHS.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
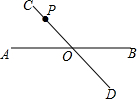 如图,直线AB、CD相交于O,P是CD上一点按要求画图并回答问题:
如图,直线AB、CD相交于O,P是CD上一点按要求画图并回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
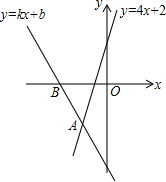 如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1.
如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
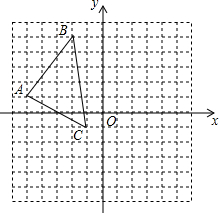 如图,在平面直角坐标系中,△ABC的顶点都在网格点上,每个小正方形边长为1个单位长度.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上,每个小正方形边长为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间(秒) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 速度(米/秒) | 0 | 0.3 | 1.3 | 2.8 | 1.9 | 7.6 | 11.0 | 14.1 | 18.4 | 24.2 | 28.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com