
在 中和
中和 中,已知
中,已知 ,
,  ,增加下列条件后还不能判定
,增加下列条件后还不能判定 ≌
≌ 的是( ).
的是( ).
A. 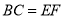 B.
B.  C.
C.  D.
D. 
科目:初中数学 来源:江苏省扬州市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
关于x的方程2(x﹣3)﹣m=2的解和方程3x﹣7=2x的解相同.
(1)求m的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,求线段AQ的长.

查看答案和解析>>
科目:初中数学 来源:河北省保定市高阳县2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年八年级上学期期末数学试卷 题型:解答题
甲、乙两车从 地驶向
地驶向 地,甲车比乙车早行驶
地,甲车比乙车早行驶 ,并且在途中休息了
,并且在途中休息了 ,休息前后速度相同,如图是甲乙两车行驶的距离
,休息前后速度相同,如图是甲乙两车行驶的距离 与时间
与时间 的函数图象,当甲车行驶__________
的函数图象,当甲车行驶__________  时,两车恰好相距
时,两车恰好相距 .
.

查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年八年级上学期期末数学试卷 题型:单选题
如图,直线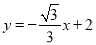 与
与 轴,
轴,  轴分别交于
轴分别交于 ,
,  两点,把
两点,把 沿着直线
沿着直线 翻折后得到
翻折后得到 ,则点
,则点 的坐标是( ).
的坐标是( ).

A.  B.
B.  C.
C. 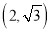 D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷(解析版) 题型:解答题
如图,已知直线 交⊙
交⊙ 于
于 、
、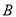 两点,
两点,  是直径,
是直径,  平分
平分 交⊙
交⊙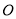 于
于 ,连接
,连接 ,过点
,过点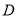 作
作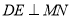 ,垂足为
,垂足为 .
.

( )求证:
)求证: 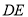 是⊙
是⊙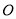 的切线.
的切线.
( )若
)若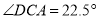 ,
, 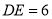 ,求
,求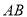 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷(解析版) 题型:解答题
质检部门对甲、乙两个厂生产的乒乓球的直径进行检测,从它们生产的乒乓球中各抽样调查了 只,把检测的结果绘成如下两幅图:
只,把检测的结果绘成如下两幅图:


( )甲厂生产
)甲厂生产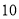 只乒乓球直径的极差是__________
只乒乓球直径的极差是__________  .乙厂生产的
.乙厂生产的 只乒乓球直径的极差是__________
只乒乓球直径的极差是__________  .
.
( )你认为哪个厂生产的
)你认为哪个厂生产的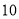 只乒乓球的直径比较稳定?请通过计算说明.
只乒乓球的直径比较稳定?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷(解析版) 题型:填空题
将二次函数 化成
化成 的形式应为__________.
的形式应为__________.
查看答案和解析>>
科目:初中数学 来源:四川省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
解下列方程(不等式)组.
(1)解方程组: 
(2) 解不等式组:  ,并求其非负整数解.
,并求其非负整数解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com