
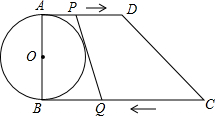
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12cm,AD=13cm,BC=22cm,AB是⊙O的直径,动点P从点A出发向点D以1cm/s的速度运动,动点Q从点C出发向点B以2cm/s的速度运动.点P、Q同时出发,其中一个点停止时,另一个点也停止运动.设运动时间为t秒.
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12cm,AD=13cm,BC=22cm,AB是⊙O的直径,动点P从点A出发向点D以1cm/s的速度运动,动点Q从点C出发向点B以2cm/s的速度运动.点P、Q同时出发,其中一个点停止时,另一个点也停止运动.设运动时间为t秒.分析 (1)当PQ是圆的切线时,利用切线的性质把AP,PH,CQ,BQ分别用t表示,然后利用勾股定理就可以求出t.
(2)根据(1)解得的结果,t=2或t=9,直线PQ从开始运动时与圆相交,一直到当t=2时,直线与圆相切;再运动时,直线与圆相离,再到t=9时,直线与圆相切,然后相交,直到停止.
解答 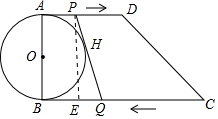 解:(1))设PQ与⊙O相切于点H过点P作PE⊥BC,垂足为E;
解:(1))设PQ与⊙O相切于点H过点P作PE⊥BC,垂足为E;
∵直角梯形ABCD,AD∥BC,
∴PE=AB,
∵AP=BE=t,CQ=2t,
∴BQ=BC-CQ=22-2t,EQ=BQ-BE=22-2t-t=22-3t;
∵AB为⊙O的直径,∠ABC=∠DAB=90°,
∴AD、BC为⊙O的切线,
∴AP=PH,HQ=BQ,
∴PQ=PH+HQ=AP+BQ=t+22-2t=22-t;
在Rt△PEQ中,PE2+EQ2=PQ2,
∴122+(22-3t)2=(22-t)2,
即:8t2-88t+144=0,
∴t2-11t+18=0,
(t-2)(t-9)=0,
∴t1=2,t2=9;
∵P在AD边运动的时间为$\frac{AD}{1}$=$\frac{13}{1}$=13秒,Q在CB边运动的时间为$\frac{BC}{2}$=$\frac{22}{2}$=11,
∴当t=2或9秒时,PQ与⊙O相切.
(2)由(1)可知PQ与⊙O相交时t的取值范围为0≤t<2 或 9<t≤11.
点评 此题考查切线的判定,直角梯形的性质,正确求得直线PQ与圆相切时t的值是关键.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:填空题
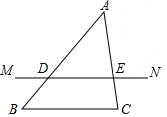 如图:直线MN∥BC,直线MN经过△ABC的重心,且直线MN交AB、AC于点D、E,那么△ADE与△ABC的相似比的值是$\frac{2}{3}$.
如图:直线MN∥BC,直线MN经过△ABC的重心,且直线MN交AB、AC于点D、E,那么△ADE与△ABC的相似比的值是$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2400×(1-20%) | B. | 2400÷(1-20%) | C. | 2400×(1+20%) | D. | 2400÷(1+20%) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=8 | B. | $\root{3}{-8}$=-2 | C. | $\sqrt{(-2)^{2}}$=-2 | D. | $\sqrt{9+\frac{1}{4}}$=3+$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB,AC分别为⊙O的直径和弦,D是$\widehat{BC}$的中点,DE⊥AC于E,DE=3,AC=8.
如图,已知AB,AC分别为⊙O的直径和弦,D是$\widehat{BC}$的中点,DE⊥AC于E,DE=3,AC=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com