
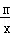 的图象如图,以下结论:
的图象如图,以下结论: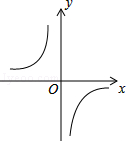
| A.4个 | B.3个 | C.2个 | D.1个 |
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源:不详 题型:解答题
 (x>0)图象上.
(x>0)图象上. 的解析式;
的解析式; 的图象上?并说明理由.
的图象上?并说明理由.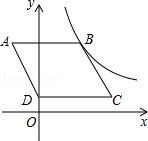
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的坐标为(
的坐标为( ,
,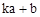 )(其中k为常数,且
)(其中k为常数,且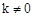 ),则称点
),则称点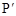 为点P的“k属派生点”.
为点P的“k属派生点”.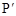 (1+
(1+ ,
,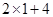 ),即
),即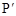 (3,6).
(3,6). 的“2属派生点”
的“2属派生点” 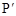 的坐标为____________;
的坐标为____________; 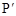 的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
的坐标为(3,3),请写出一个符合条件的点P的坐标____________;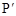 点,且△
点,且△ 为等腰直角三角形,则k的值为____________;
为等腰直角三角形,则k的值为____________;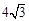 ),点A在函数
),点A在函数 的图象上,且点A是点B的“
的图象上,且点A是点B的“ 属派生点”,当线段B Q最短时,求B点坐标.
属派生点”,当线段B Q最短时,求B点坐标.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
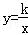 (x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )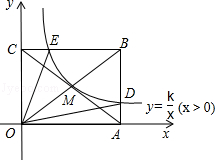
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x2 |
| x-1 |
| x2+2x |
| x2-4 |
| 2 |
| x-2 |
| x |
| x+1 |
| 3x |
| x-1 |
| x |
| x2-1 |
| 2b |
| a-b |
| 2b |
| a+b |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
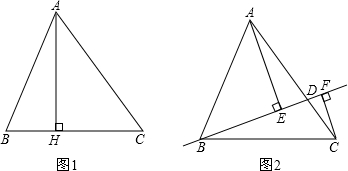
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 (x>0)的图象上有点P1、P2、P3…、Pn、Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn,则S1= _______ ,Sn= _________ .(用含n的代数式表示)
(x>0)的图象上有点P1、P2、P3…、Pn、Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn,则S1= _______ ,Sn= _________ .(用含n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com