
【题目】在ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F,且BE=DF.
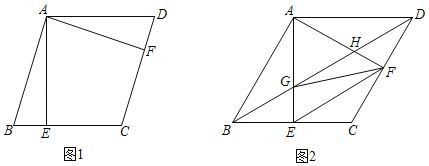
(1)如图1,求证:ABCD是菱形;
(2)如图2,连接BD,交AE于点G,交AF于点H,连接EF、FG,若∠CEF=30°,在不添加任何字母及辅助线的情况下,请直接写出图中面积是△BEG面积2倍的所有三角形.
【答案】(1)见解析;(2)△ABG、△ADH、△AGH、△DFG
【解析】
(1)证明△AEB≌△AFD得出AB=AD,即可得出结论;
(2)连接AC交BD于O,则AC⊥BD,证出EF∥BD,得出∠CBD=∠CEF=30°,∠ABC=60°,证明△ABC是等边三角形,∠EBG=∠FDH,得出∠BAG=∠ABG,∴AG=BG,同理:AH=DH,得出BE=![]() BC=
BC=![]() AB,由菱形的性质和角平分线的性质得出点G到AB与BC边上的高相等,得出S△ABG=2S△BEG;证明△BEG≌△DFH得出BG=DH,得出AG=AH,得出S△ABG=S△ADH,S△ADH=2S△BEG;证出△AGH是等边三角形,得出GH=AG=AH=BG=DH,OG=
AB,由菱形的性质和角平分线的性质得出点G到AB与BC边上的高相等,得出S△ABG=2S△BEG;证明△BEG≌△DFH得出BG=DH,得出AG=AH,得出S△ABG=S△ADH,S△ADH=2S△BEG;证出△AGH是等边三角形,得出GH=AG=AH=BG=DH,OG=![]() AG=EG,OA=
AG=EG,OA=![]() OG=BE,得出△AGH的面积=2△BEG的面积;△GHF的面积=△DFH的面积,得出△DFG的面积=2△BEG的面积.
OG=BE,得出△AGH的面积=2△BEG的面积;△GHF的面积=△DFH的面积,得出△DFG的面积=2△BEG的面积.
解:(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
在△AEB和△AFD中, ,
,
∴△AEB≌△AFD(ASA),
∴AB=AD,
∴ABCD是菱形;
(2)解:图中面积是△BEG面积2倍的所有三角形为△ABG、△ADH、△AGH、△DFG;理由如下:
连接AC交BD于O,如图所示:
则AC⊥BD,
∵BC=CD,BE=DF,
∴BE:BC=DF:CD,
∴EF∥BD,
∴∠CBD=∠CEF=30°,
∴∠ABC=60°,
∵ABCD是菱形,
∴BC=CD=AB,
∴△ABC是等边三角形,∠EBG=∠FDH,
∴∠BAG=∠ABG,
∴AG=BG,
同理:AH=DH,
∵AE⊥BC,
∴BE=![]() BC=
BC=![]() AB,
AB,
∵ABCD是菱形,
∴BD是∠ABC的平分线,
∴点G到AB与BC边上的高相等,
∴S△ABG=2S△BEG,
在△BEG和△DFH中, ,
,
∴△BEG≌△DFH(ASA),
∴△BEG的面积=△DFH的面积,BG=DH,
∴AG=AH,
∵△AEB≌△AFD,
∴S△ABG=S△ADH,∴S△ADH=2S△BEG;
∵∠GAH=∠OAG+∠OAH=60°,
∴△AGH是等边三角形,
∴GH=AG=AH=BG=DH,OG=![]() AG=EG,OA=
AG=EG,OA=![]() OG=BE,
OG=BE,
∴△AGH的面积=2△BEG的面积,
∴△GHF的面积=△DFH的面积,
∴△DFG的面积=2△BEG的面积;
∴图中面积是△BEG面积2倍的三角形为:△ABG、△ADH、△AGH、△DFG.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上,若抛物线y=-x2-5x+c经过点B、C,则菱形ABCD的面积为( )
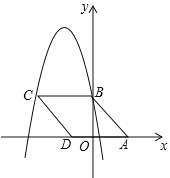
A.15B.20C.25D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(1,2)和点B(4,5),当直线y=kx﹣2k(k为常数)与线段AB有交点时,k的取值范围为( )
A.k≤﹣2或k≥![]() B.﹣2≤k≤
B.﹣2≤k≤![]()
C.﹣2≤k≤0或0≤k≤![]() D.﹣2<k<0或0<k<
D.﹣2<k<0或0<k<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,以点![]()
![]() 为圆心,以3为半径的圆,分别交
为圆心,以3为半径的圆,分别交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 轴负半轴于点
轴负半轴于点![]()
![]() .
.
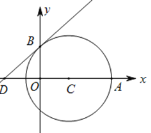
(1)求![]() 两点的坐标;
两点的坐标;
(2)求证:直线![]() 是⊙
是⊙![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,下列结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若B(﹣5,y1)、C(﹣1,y2)为函数图象上的两点,则y1<y2.其中正确结论是( )

A.②④B.①③④C.①④D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
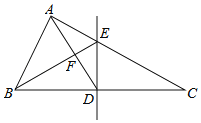
【题目】如图,在△ABC中,BC的垂直平分线分别交BC、AC于点D、E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由;
(2)BC=6,DE=2,求△BFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与函数
的图象与函数![]() (
(![]() )的图象相交于点
)的图象相交于点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() .点
.点![]() 是线段
是线段![]() 上一点,
上一点,![]() 与
与![]() 的面积比为2:3.
的面积比为2:3.
(1)![]() ,
,![]() ;
;
(2)求点![]() 的坐标;
的坐标;
(3)若将![]() 绕点
绕点![]() 顺时针旋转,得到
顺时针旋转,得到![]() ,其中
,其中![]() 的对应点是
的对应点是![]() ,
,![]() 的对应点是
的对应点是![]() ,当点
,当点![]() 落在
落在![]() 轴正半轴上,判断点
轴正半轴上,判断点![]() 是否落在函数
是否落在函数![]() (
(![]() )的图象上,并说明理由.
)的图象上,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,建筑物AB的高为6cm,在其正东方向有个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A、塔项C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() =1.73,精确到0.1m)
=1.73,精确到0.1m)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com