
某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售价格x(元/个)的变化如下表:
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
解:(1)根据表格中数据可得出:y与x是一次函数关系,设解析式为:y=ax+b,
则 ,解得:
,解得: 。
。
∴函数解析式为:y= x+8。
x+8。
(2)根据题意得:
z=(x﹣20)y﹣40=(x﹣20)( x+8)﹣40=
x+8)﹣40= x2+10x﹣200=
x2+10x﹣200= (x2﹣100x)﹣200
(x2﹣100x)﹣200
= [(x﹣50)2﹣2500]﹣200=
[(x﹣50)2﹣2500]﹣200= (x﹣50)2+50,
(x﹣50)2+50,
∵ <0,∴x=50,z最大=50。
<0,∴x=50,z最大=50。
∴该公司销售这种计算器的净得利润z与销售价格x)的函数解析式为z= x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元。
x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元。
(3)当公司要求净得利润为40万元时,即 (x﹣50)2+50=40,解得:x1=40,x2=60。
(x﹣50)2+50=40,解得:x1=40,x2=60。
作函数图象的草图,
通过观察函数y= (x﹣50)2+50的图象,可知按照公司要求使净得利润不低于40万元,则销售价格的取值范围为:40≤x≤60.
(x﹣50)2+50的图象,可知按照公司要求使净得利润不低于40万元,则销售价格的取值范围为:40≤x≤60.
而y与x的函数关系式为:y= x+8,y随x的增大而减少,
x+8,y随x的增大而减少,
∴若还需考虑销售量尽可能大,销售价格应定为40元/个。
解析试题分析:(1)根据数据得出y与x是一次函数关系,进而利用待定系数法求一次函数解析式。
(2)根据z=(x﹣20)y﹣40得出z与x的函数关系式,应用二次函数最值原理求解即可。
(3)首先求出40= (x﹣50)2+50时x的值,从而二次函数的性质根据得出x(元/个)的取值范围,结合一次函数的性质即可求得结果。
(x﹣50)2+50时x的值,从而二次函数的性质根据得出x(元/个)的取值范围,结合一次函数的性质即可求得结果。


科目:初中数学 来源: 题型:解答题
某公司营销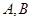 两种产品,根据市场调研,发现如下信息:
两种产品,根据市场调研,发现如下信息:
信息1:销售 种产品所获利润
种产品所获利润 (万元)与所售产品
(万元)与所售产品 (吨)之间存在二次函数关系
(吨)之间存在二次函数关系 .当
.当 时,
时, ;当
;当 时,
时, .
.
信息2:销售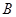 种产品所获利润
种产品所获利润 (万元)与所售产品
(万元)与所售产品 (吨)之间存在正比例函数关系
(吨)之间存在正比例函数关系 .
.
根据以上信息,解答下列问题:(1)求二次函数解析式;
(2)该公司准备购进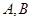 两种产品共10吨,请设计一个营销方案,使销售
两种产品共10吨,请设计一个营销方案,使销售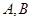 两种产品获得的利润之和最大,最大利润是多少?
两种产品获得的利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图形L.
(1)求△ABC的面积;
(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;
(3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
| 销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
| x | 3000 | 3200 | 3500 | 4000 |
| y | 100 | 96 | 90 | 80 |
| 租出的车辆数 | | 未租出的车辆数 | |
| 租出每辆车的月收益 | | 所有未租出的车辆每月的维护费 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
(1)求点A,B的坐标(直接写出结果),并证明△MDE是等腰三角形;
(2)△MDE能否为等腰直角三角形?若能,求此时点P的坐标;若不能,说明理由;
(3)若将“P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上)”改为“P是抛物线在x轴下方的一个动点”,其他条件不变,△MDE能否为等腰直角三角形?若能,求此时点P的坐标(直接写出结果);若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系中,一个二次函数的图象经过点A(1,0)、B(3,0)两点.
(1)写出这个二次函数的对称轴;
(2)设这个二次函数的顶点为D,与y轴交于点C,它的对称轴与x轴交于点E,连接AD、DE和DB,当△AOC与△DEB相似时,求这个二次函数的表达式。
[提示:如果一个二次函数的图象与x轴的交点为 A,那么它的表达式可表示为:
A,那么它的表达式可表示为: ]
]
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,△ABC中,AB=BC,AC=8,tanA=k,P为AC边上一动点,设PC=x,作PE∥AB交BC于E,PF∥BC交AB于F.
(1)证明:△PCE是等腰三角形;
(2)EM、FN、BH分别是△PEC、△AFP、△ABC的高,用含x和k的代数式表示EM、FN,并探究EM、FN、BH之间的数量关系;
(3)当k=4时,求四边形PEBF的面积S与x的函数关系式.x为何值时,S有最大值?并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
直线 与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
(1)求抛物线的解析式;
(2)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com