
 如图,在△ABC中,AB=AC=2,∠BAC=120°,以AB为直径的⊙O交BC于点M,MN⊥AC于点N,图中阴影部分的面积为( )
如图,在△ABC中,AB=AC=2,∠BAC=120°,以AB为直径的⊙O交BC于点M,MN⊥AC于点N,图中阴影部分的面积为( )| A. | $\frac{3\sqrt{3}}{4}$-$\frac{π}{6}$ | B. | $\frac{3\sqrt{3}}{8}$-$\frac{π}{6}$ | C. | $\frac{3\sqrt{3}}{4}$-$\frac{π}{12}$ | D. | $\frac{3\sqrt{3}}{8}$-$\frac{π}{12}$ |
分析 先证明MN为⊙O切线,求阴影部分的面积要把它转化成S梯形ANMO-S扇形OAM,再分别求的这两部分的面积求解.
解答 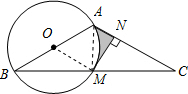 解:证明:连接OM.
解:证明:连接OM.
∵OM=OB,
∴∠B=∠OMB.
∵AB=AC,
∴∠B=∠C.
∴∠OMB=∠C.
∴OM∥AC.
∵MN⊥AC,
∴OM⊥MN.
∵点M在⊙O上,
∴MN是⊙O的切线;
连接AM.
∵AB为直径,点M在⊙O上,
∴∠AMB=90°.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∴∠AOM=60°.
又∵在Rt△AMC中,MN⊥AC于点N,
∴∠AMN=30°.
∴AN=AM•sin∠AMN=AC•sin30°•sin30°=$\frac{1}{2}$.
∴MN=AM•cos∠AMN=AC•sin30°•cos30°=$\frac{\sqrt{3}}{2}$.
∴S梯形ANMO=$\frac{(AN+OM)•MN}{2}$=$\frac{3\sqrt{3}}{8}$,
S扇形OAM=$\frac{60π•{1}^{2}}{360}$=$\frac{π}{6}$,
∴S阴影=$\frac{9\sqrt{3}-4π}{24}$=$\frac{3\sqrt{3}}{8}$-$\frac{π}{6}$.
故选B.
点评 本题考查了圆周角定理、等腰三角形的性质以及扇形面积的计算,明确切线的判定即利用图形分割法求不规则图形面积是解题的思路.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx(a≠0)的顶点(-1,m)(m>0),则下列结论中,正确的是( )
如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx(a≠0)的顶点(-1,m)(m>0),则下列结论中,正确的是( )| A. | a+b=k | B. | 2a+b=0 | C. | b<k<0 | D. | k<a<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+6x-7=0可化为(x+3)2=2 | B. | x2-2x-9=0可化为(x-1)2=8 | ||
| C. | x2+8x-9=0可化为(x+4)2=16 | D. | x2-4x=0可化为(x-2)2=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=17 | B. | (x-3)2=1 | ||
| C. | (x+3)2=17?????????? | D. | (x+3)2=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<4且m≠0 | B. | m<-4 | C. | m>-4且m≠0 | D. | m>4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 分数(分) | 60 | 70 | 80 | 90 | 100 |
| 人数(分) | 1 | 1 | 5 | 2 | 1 |
| A. | 学生成绩的方差是110 | B. | 学生成绩的众数是5 | ||
| C. | 学生成绩的中位数是80分 | D. | 学生成绩的平均数是80分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com