
【题目】甲、乙两人加工同一种机器零件,甲比乙每小时多加工10个零件,甲加工150个零件所用的时间与乙加工120个零件所用时间相等
(1)求甲、乙两人每小时各加工多少个机器零件?
【答案】
(1)
解:设乙每小时加工机器零件x个,则甲每小时加工机器零件(x+10)个,根据题意得: ![]() ,
,
解得x=40,
经检验,x=40是原方程的解,
x+10=40+10=50.
答:甲每小时加工50个零件,乙每小时加工40个零件。
;
解:设乙每小时加工机器零件x个,则甲每小时加工机器零件(x+10)个,根据题意得: ![]() ,
,
解得x=40,
经检验,x=40是原方程的解,
x+10=40+10=50.
答:甲每小时加工50个零件,乙每小时加工40个零件。
;解:设乙每小时加工机器零件x个,则甲每小时加工机器零件(x+10)个,根据题意得: ![]() ,
,
解得x=40,
经检验,x=40是原方程的解,
x+10=40+10=50.
答:甲每小时加工50个零件,乙每小时加工40个零件。
【解析】根据“甲加工150个零件所用的时间与乙加工120个零件所用时间相等”可得出相等关系,从而只需表示出他们各自的时间就可以了.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算AC2+BC2的值等于 ;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个平行四边形ABEF,使得该平行四边形的面积等于16;
(3)请在如图所示的网格中,用无刻度的直尺,画出一个矩形ABMN,使得该矩形的面积等于AC2+BC2.


查看答案和解析>>
科目:初中数学 来源: 题型:
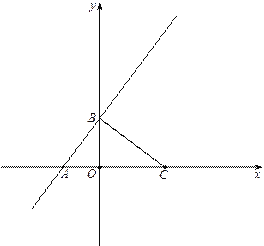
【题目】如图,在平面直角坐标系xOy中,点C的坐标为(4,0),一次函数![]() 的图像分别交x轴、y轴于点A、点B.
的图像分别交x轴、y轴于点A、点B.
⑴ 若点D是直线AB在第一象限内的点,且BD=BC,试求出点D的坐标.
⑵ 在⑴的条件下,若点Q是坐标轴上的一个动点,试探索在第一象限是否存在另一个点P,使得以B、D、P、Q为顶点的四边形是菱形(BD为菱形的一边)?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.

(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作 MG⊥EF交线段BC于点G,判断△GEF的形状,并说明理由;
(3)如图3,若AB= ![]() ,过点M作 MG⊥EF交线段BC的延长线于点G.
,过点M作 MG⊥EF交线段BC的延长线于点G.
①直接写出线段AE长度的取值范围;
②判断△GEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3![]() ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+![]() .其中正确的结论是
.其中正确的结论是

A. ①②③⑤ B. ①③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.

(1)、求证:四边形BFDE是平行四边形;
(2)、若四边形BFDE是菱形, AB=2,求菱形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(徐州中考)如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长交DC于点F,求证:
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
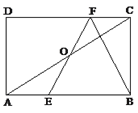
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC。
(1)求证;OE=OF;(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com