
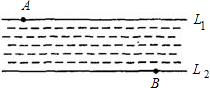
 如图,河岸上L1∥L2,位置A位于L1上,位置B位于L2上,A、B的水平距离为120米,垂直距离为30米.小刚要从A游泳过河再步行到B.已知步行速度是游泳速度的2倍.八年级的小刚学以致用,先设计了如下甲、乙、丙三个方案,你认为哪个方案费时最少?说明理由.(只考虑游泳和步行时间,其它时间忽略不计,以下数据供选用:
如图,河岸上L1∥L2,位置A位于L1上,位置B位于L2上,A、B的水平距离为120米,垂直距离为30米.小刚要从A游泳过河再步行到B.已知步行速度是游泳速度的2倍.八年级的小刚学以致用,先设计了如下甲、乙、丙三个方案,你认为哪个方案费时最少?说明理由.(只考虑游泳和步行时间,其它时间忽略不计,以下数据供选用:| 2 |
| 3 |
| 1800 |
| 300 |
| 2 |


科目:初中数学 来源: 题型:解答题
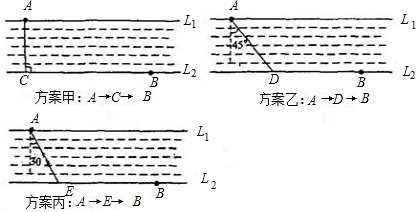
 如图,河岸上L1∥L2,位置A位于L1上,位置B位于L2上,A、B的水平距离为120米,垂直距离为30米.小刚要从A游泳过河再步行到B.已知步行速度是游泳速度的2倍.八年级的小刚学以致用,先设计了如下甲、乙、丙三个方案,你认为哪个方案费时最少?说明理由.(只考虑游泳和步行时间,其它时间忽略不计,以下数据供选用:
如图,河岸上L1∥L2,位置A位于L1上,位置B位于L2上,A、B的水平距离为120米,垂直距离为30米.小刚要从A游泳过河再步行到B.已知步行速度是游泳速度的2倍.八年级的小刚学以致用,先设计了如下甲、乙、丙三个方案,你认为哪个方案费时最少?说明理由.(只考虑游泳和步行时间,其它时间忽略不计,以下数据供选用: ≈1.414,
≈1.414, ≈1.732,
≈1.732,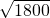 ≈42.42,
≈42.42,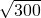 ≈17.32)
≈17.32)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com