
【题目】一个菱形两条对角线长的和是10,菱形的面积是12,则菱形的边长为_____.
【答案】![]()
【解析】
由菱形的性质得出AB=BC=CD=DA,AC⊥BC,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,由菱形的性质和已知条件得出ACBD=24①,由勾股定理得出AB2=
BD,由菱形的性质和已知条件得出ACBD=24①,由勾股定理得出AB2=![]() (AC2+BD2),AC+BD=10②,由①②得出AC2+BD2=56,得出AB2=13,即可得出结果.
(AC2+BD2),AC+BD=10②,由①②得出AC2+BD2=56,得出AB2=13,即可得出结果.
解:如图所示:

∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AC⊥BC,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴∠AOB=90°,菱形ABCD的面积=![]() ACBD=12,
ACBD=12,
∴ACBD=24①,AB2=OA2+OB2=![]() (AC2+BD2),
(AC2+BD2),
∵菱形两条对角线长的和是10,
∴AC+BD=10②,
由②2-2×①得:AC2+BD2=56,
∴![]() (AC2+BD2)=13,
(AC2+BD2)=13,
∴AB2=13,
∴AB=![]() ,
,
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)若∠AOE=32°,求∠BOC的度数;
(2)若OD是∠AOC的角平分线,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸上的每个小方格都是边长为1的正方形,△ABC 的顶点均在格点上,若 B
点的坐标为(-4,-2), 按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点A和点C的坐标;
(3)画出△ABC关于x轴的对称图形△ABC;
(4)△ABC 的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家在学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可 以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.学有所用:在等腰 三角形 ABC中,AB=AC,其一腰上的高为h,M 是底边BC上的任意一点,M 到腰AB、AC 的距离分别为 h1、h2 .
(1)请你结合图形来证明: h1+h2=h;
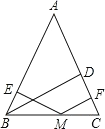
(2)当点M在BC延长线上时,h1、h2、h 之间又有什么样的结论.请你画出图形,并直
接写出结论不必证明;
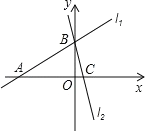
(3)利用以上结论解答,如图在平面直角坐标系中有两条直线l1:y=x+3,l2:y=-3x+3
若 l2上的一点M 到l1的距离是![]() ,求点 M 的坐标.
,求点 M 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
x﹣2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( ) 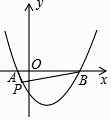
A.﹣1<m<0
B.﹣1<m<0或3<m<4
C.0<m<3或m>4
D.m<﹣1或0<m<3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com