
 如图,Rt△ACB中,∠C=90°,AC=12,BC=5,等腰Rt△DEF的顶点D、E分别在边AC、AB上,且ED⊥AC于点D,连接AF并延长交BC于点G.已知DE=EF=2,则BG的长为( )
如图,Rt△ACB中,∠C=90°,AC=12,BC=5,等腰Rt△DEF的顶点D、E分别在边AC、AB上,且ED⊥AC于点D,连接AF并延长交BC于点G.已知DE=EF=2,则BG的长为( )| A. | $\frac{25}{17}$ | B. | $\frac{30}{17}$ | C. | $\frac{17}{12}$ | D. | $\frac{19}{12}$ |
分析 先证明△EDA∽△BCA,得$\frac{ED}{BC}=\frac{AD}{AC}=\frac{AE}{AB}$,求AD=$\frac{24}{5}$,再证明△EFD∽△DAO,得$\frac{EF}{AD}=\frac{EO}{OD}$=$\frac{2}{\frac{24}{5}}$=$\frac{5}{12}$,设EO=5x,OD=12x,由DE=2列式得x的值,求出OE的长,最后利用$\frac{EO}{BG}=\frac{AE}{AB}=\frac{2}{5}$,求BG的长即可.
解答  解:∵ED⊥AC,BC⊥AC,
解:∵ED⊥AC,BC⊥AC,
∴ED∥BC,
∴△EDA∽△BCA,
∴$\frac{ED}{BC}=\frac{AD}{AC}=\frac{AE}{AB}$,
∵BC=5,AC=12,
∴AB=13,
∵△EFD是等腰直角三角形,
∴∠FED=90°,EF=ED=2,
∴$\frac{2}{5}=\frac{AD}{12}=\frac{AE}{AB}$,
∴AD=$\frac{24}{5}$,
∵∠FED=∠EDA=90°,
∴EF∥AD,
∴△EFD∽△DAO,
∴$\frac{EF}{AD}=\frac{EO}{OD}$=$\frac{2}{\frac{24}{5}}$=$\frac{5}{12}$,
设EO=5x,OD=12x,
∴5x+12x=2,
x=$\frac{2}{17}$,
∴EO=5x=$\frac{10}{17}$,
∵EO∥BG,
∴$\frac{EO}{BG}=\frac{AE}{AB}=\frac{2}{5}$,
∴$\frac{\frac{10}{17}}{BG}=\frac{2}{5}$,
∴BG=$\frac{25}{17}$,
故选A.
点评 本题考查了相似三角形的性质和判定、等腰直角三角形的性质,熟练掌握平行相似的判定方法,根据相似三角形对应边成比例列等式求线段的长,从而使问题得以解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
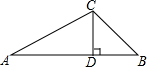 南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)
南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
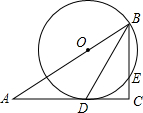 如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 目的地 | 运费/(元/t) | |
| 甲仓库 | 乙仓库 | |
| A地 | 140 | 200 |
| B地 | 100 | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com